Thermisch effiziente Tiegeltechnologie
Grundlagen, Modellbildung und Anwendungen für Energieeinsparungen
Von Brian Pinto und Wenwu Shi, Pittsburgh und Steffen Heumann, Großalmerode

2-D- und 3-D-Computermodelle ermöglichen die effektive Untersuchung zur Optimierung von Tiegelmaterial und -design bezüglich Wärmeflussverhalten und Energieeffizienz.
Erschienen in GIESSEREI 07/2019
Um die energetischen Verhältnisse in Tiegeln zu simulieren, die in Aluminiumgießereien verwendet werden, wurden auf Basis von detaillierten Materialdaten multivariate mathematische Modelle erstellt. Ziel war es, die Auswirkungen von Änderungen der Tiegelgeometrie und der Werkstoffeigenschaften auf die Gesamtenergiebilanz des Ofens beim Schmelzen und Warmhalten von Metall zu untersuchen. Dabei war es insbesondere auch wichtig, den Einfluss der thermischen Eigenschaften auf die Energieeffizienz und die thermischen Spannungen zu verstehen. Probleme bei der Bewertung dieser Parameter für die Gießereipraxis ergeben sich aus der Schwierigkeit, äußere Faktoren, die sich ebenfalls auf die Ofenleistung auswirken, wie z.B. individuelle Konfigurationen, Ofenzustand und etwaige schlechte Betriebsbedingungen, herauszurechnen. Da das Schmelzen und Warmhalten von Metall in Tiegeln einen großen Teil des Energiebedarfs der Gießerei-Industrie ausmacht, könnten die jüngsten Fortschritte bei den Tiegeltechnologien die Kosteneffizienz und den CO2-Fußabdruck in der gesamten Branche erheblich beeinflussen.
Grundlagen
Die zum Schmelzen und Warmhalten von Metall verwendete Energie macht fast 40 % der Energiekosten einer herkömmlichen Gießerei aus [1]. Die Gießerei-Industrie ist bekannt für hohen Energiebedarf, geringe Energieeffizienz und hohe CO2-Emissionen [2-4]. Dabei liegt der Energieverbrauch im Durchschnitt weit über dem, was nach theoretischen Berechnungen prognostiziert wird [5-7]. Dies ist auf Schwächen beim Zusammenspiel des Schmelzens und Gießens zurückzuführen, die teils im Prozess selbst begründet sind, aber auch von den verwendeten Anlagentypen und spezifischen Methoden abhängen. Es gibt Möglichkeiten, die Energieeffizienz eines Gießereibetriebs zu verbessern, die Umweltbelastung deutlich zu reduzieren und gleichzeitig die Wettbewerbsfähigkeit der Branche zu erhalten [8-10].
Eine der gebräuchlichsten Methoden zum Schmelzen von Metallen ist ein elektrischer Widerstandsofen oder ein mit Brennstoff befeuerter Ofen [11,12]. In diesen Öfen wird geschmolzenes Metall in großen feuerfesten Tiegeln bei hohen Temperaturen warmgehalten. Zum Schmelzen wird die Energie, die durch Widerstandselemente oder durch Verbrennung an der Tiegelaußenwand erzeugt wird, auf die Metallcharge im Inneren geleitet und anschließend wird diese bei hohen Temperaturen geschmolzen [11,12]. Literaturstudien zeigen, dass empfohlene energiesparende Maßnahmen zur Optimierung der Ofenkonfiguration und / oder zur Verbesserung der Schmelzleistung [13-16] wenig oder gar keinen Fokus auf den Tiegel haben.
Wenn Metall geschmolzen wird, verbraucht ein gut isolierter Ofen nur nominale Energie, um die Schmelze auf einer bestimmten Temperatur zu halten und Wärmeverluste an die Umgebung auszugleichen. Um zu diesem Punkt zu gelangen, ist jedoch eine enorme Menge an Wärmeenergie erforderlich, nicht nur, um das Metall auf seine Liquidustemperatur zu bringen und es zu schmelzen, sondern auch, um diese Wärme durch ein dickes, hochemissionsfähiges keramisches Material mit hoher spezifischer Wärmekapazität zu leiten, während es gleichzeitig den thermodynamischen Kräften entgegenwirkt, die den Wärmeabtransport in die Atmosphäre begünstigen.
Während beim Schmelzen eine schnelle Wärmeleitung durch den Tiegel wünschenswert ist, soll sie beim Halten möglichst langsam sein. Wird ein Tiegel sowohl für Schmelz- als auch für Warmhalteanwendungen innerhalb desselben Ofens verwendet, wird die Herausforderung, ein universell effizientes Schmelzgefäß zu schaffen, größer. Darüber hinaus sind die Methoden der Kunden in der gesamten Branche so unterschiedlich, dass selbst die Abstimmung der Effizienz eines Ofens mit dem eigenen Tiegel äußerst schwierig wird. Wenn beispielsweise ein Ofen eine schlechte Isolierung aufweist, wird der Effekt des Wechsels zu einem hocheffizienten Tiegel durch die grobe Ineffizienz des Ofens zunichtegemacht. Dies wurde in vielen Feldversuchen beobachtet. Die thermische Wirkung eines Tiegels zu untersuchen und nachzuweisen, ist in der Praxis also kaum möglich. Mit theoretischen Modellen auf Basis von Finite-Elemente-Analysemethoden lässt sich jedoch sehr gut untersuchen, wie Wärmeflussverhalten und Energieeffizienz allein auf der Grundlage von Änderungen der Eigenschaften des Tiegelmaterials und des Designs beeinflusst werden können. Dabei werden die Vorteile fortschrittlicher Tiegeltechnologien deutlich.
Versuchsaufbau
Die Finite-Elemente-Analyse (FEA) wurde mit dem ABAQUS-6.11-Paket für Wärmeübertragung und Temperaturverschiebung durchgeführt. Basierend auf dem Modell für einen typischen schüsselförmigen Tiegel (z.B. BU500), der mit 400 kg geschmolzenem Aluminium gefüllt ist, wurde ein zweidimensionales Wärmeflussmodell erstellt. Ein dreidimensionales Modell basierte auf einem 100-kWElektro-Widerstands-Tiegelofen, aus dem Temperatur- und Energieverbrauchsdaten abgeleitet wurden. Für die Simulation in den Computermodellen wurden mehrere Tiegeltypen betrachtet, darunter sowohl Kohlenstoff- als auch Keramik-(Ton)-gebundene Varianten. Wie bei jeder Computersimulation wurden für die Entwicklung des realistischsten Modells zuverlässige „reale“ Daten benötigt, um die zu prüfenden Materialien zu beschreiben. An Proben wurden unterschiedliche Eigenschaften wie Schüttdichte, Porosität, relative Dichte, Bruchmodul (MOR), Elastizitätsmodul (Young‘s), Wärmeleitfähigkeit und spezifische Wärmekapazität bestimmt (Tabelle 1). Die aus Kundenversuchen gewonnenen Energiedaten wurden mit einem kundenspezifischen Energieüberwachungsgerät (FCTM-2, Foseco) erfasst, das gleichzeitig den Energieverbrauch und den Schmelzedurchsatz am Ofen überwachen kann.
Tabelle 1: Liste der Materialeigenschaften für die thermomechanische Modellierung von Tiegeln
| Eigenschaft | Einheit | Temperatur in °C | Referenz, ASTM-Standard |
| Rohdichte | g/cm3 | 25 | C830-00 |
| Oberflächenporosität | % | 25 | C830-00 |
| Spezifisches Gewicht | - | 25 | C830-00 |
| Biegefestigkeit | MPa | 25; 800;1200 | 78-02 |
| Elastizitätsmodul | GPa | 25 - 1600 | E1875-13 |
| Wärmeleitfähigkeit | W/m·K | 200 - 1000 | E1461-13 |
| Spezifische Wärmekapazität | J/kg·K | 200 - 1000 | E1461-13 |
Ergebnisse und Diskussion
2-D-Berechnungsmodell
Ein zweidimensionales, achsensymmetrisches Modell wurde speziell für die Untersuchung der Auswirkungen von Änderungen an Tiegeln (d.h. Geometrie; feuerfeste Eigenschaften) auf den Wärmefluss und die Schmelzleistung von Aluminium konstruiert. Es geht davon aus, dass ein kontinuierlicher, gleichmäßiger Wärmestrom auf die Außenseite eines Tiegels aufgebracht wird (Bild 1), der teilweise mit Aluminium gefüllt ist, was die Einbeziehung der Strahlungswärmeübertragung von einer Schmelzbadoberfläche und der oberen Innenwand des Tiegels ermöglicht (Bild 1b).
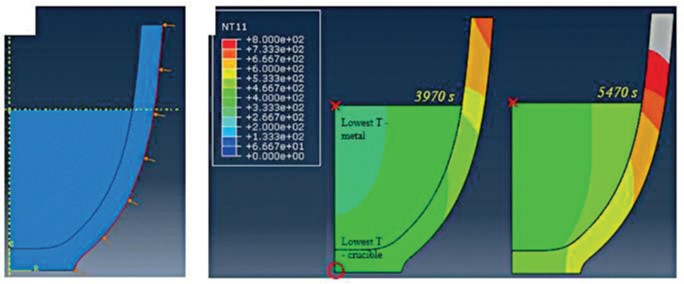
Fehlt am oberen Wandbereich des Tiegels Metall, das Wärme aufnimmt, kann die Wärme nur durch Strahlung oder Abwärtsleitung durch die Wand abgeführt werden. Es besteht die Gefahr, dass sich durch lokale Überhitzung Temperaturschockrisse bilden. Real ist die Gefahr jedoch weniger hoch, da das Modell von einem gleichmäßigen Wärmefluss ausgeht, in einem echten Ofen die Heizelemente aber typischerweise kürzer sind als der Tiegel hoch ist. Die obere Wand wird also geringer erwärmt, als berechnet.
Dadurch werden zwar Überhitzungsprobleme gemildert, aber es entsteht tendenziell das Gegenteil - eine lokale Unterkühlung, die zu schlechtem Glasurschutz, Oxidation und eventuellen Thermoschockrissen führt. Die beste Vorgehensweise ist, den Ofen so zu betreiben, dass bei diesen beiden Phänomenen ein Gleichgewicht erreicht wird: Die Füllstände sollten so hoch wie möglich sein, um steile Temperaturgradienten entlang der Tiegelwand zu vermeiden. Mittig auf der Unterseite des Tiegels (Bild 1b) befindet sich seine niedrigste relative Temperatur, da er sich hier am langsamsten erwärmt. Innerhalb des Aluminiums befindet sich die niedrigste Temperaturposition in der oberen Mitte (Bild 1b) aufgrund des Abstands zu den Elementen in Verbindung mit dem Wärmeverlust durch die Oberflächenstrahlung. Da die Wärmeleitfähigkeit von Aluminium jedoch viel höher ist als bei feuerfesten Materialien, ist der Temperaturgradient im Metall viel geringer als innerhalb der Tiegelwände.
Einflussfaktor Tiegelmaterial
Zur Bestimmung des Einflusses des Tiegelmaterials wurde für verschiedene Zusammensetzungen (A-F), sowie reines Grafit (G) als Referenzmaterial, jeweils die gleiche Heizsimulation durchgeführt, welche sich auf den Punkt der niedrigsten Aluminiumtemperatur („x“ in Bild 1b) konzentriert (Bild 2). Dabei hat jede Kurve drei verschiedene Bereiche (Bild 2a):
- (I) Die Temperatur steigt aufgrund der schnellen Wärmeleitung durch massives Aluminium sehr schnell an.
- (II) Bei Erreichen der Solidustemperatur (557 °C) nimmt die Steigung aufgrund der beim Schmelzen aufgenommenen latenten Wärme (Hf = 398 kJ / kg) deutlich ab.
- (III) Bei Überschreitung des Liquidus (613 °C) beginnt die Temperatur wieder schnell zu steigen.
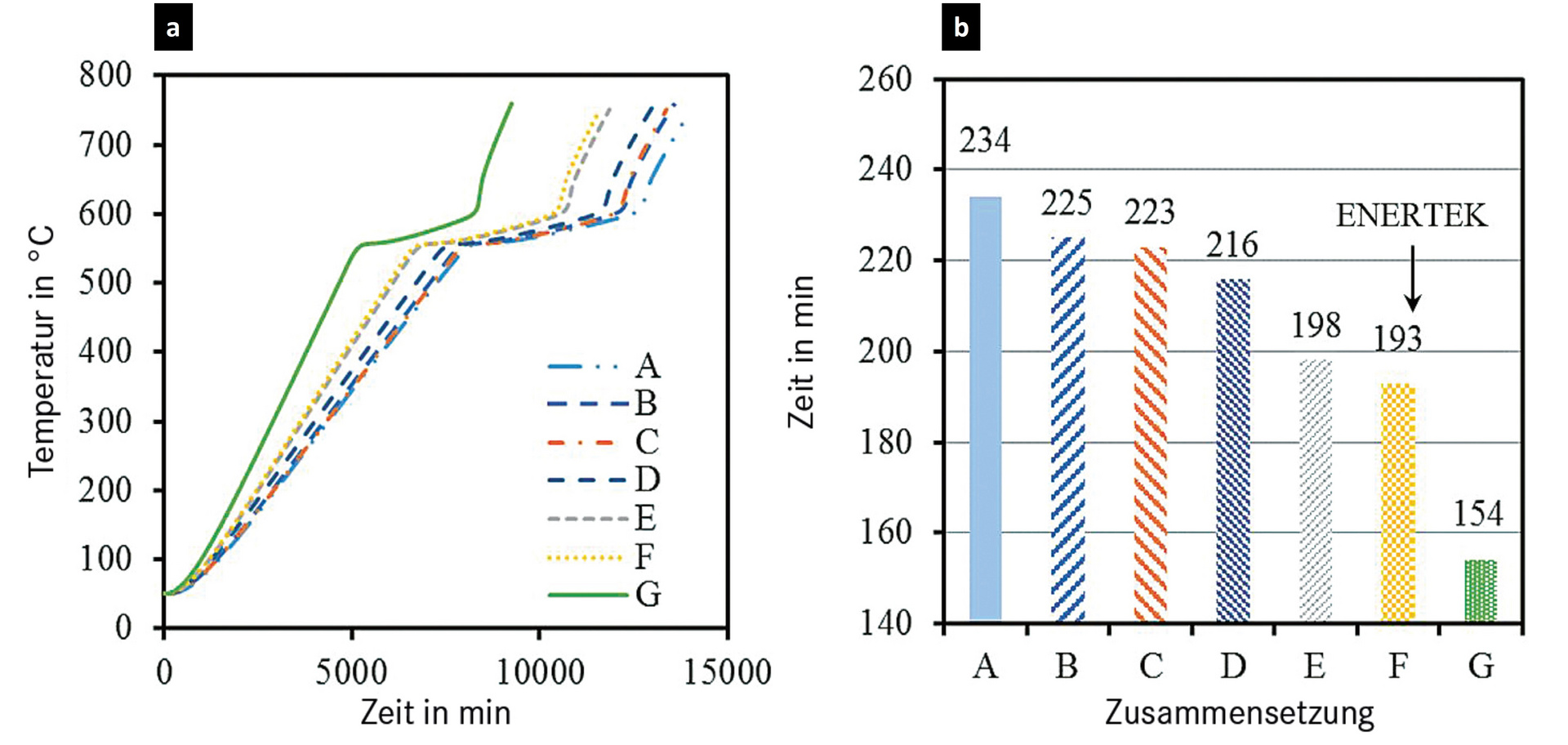
So wird es auch möglich, die Zeit vorherzusagen, die benötigt wird, um eine bestimmte Aluminiummenge in Abhängigkeit von der Tiegelzusammensetzung vollständig zu schmelzen (Bild 2b).
Der Grund für die Unterschiede in den Schmelzzeiten liegt in mehreren wichtigen Eigenschaften, die durch eine geeignete Entwicklung auf die Herstellung eines thermisch effizienteren Materials zugeschnitten werden können. Maßgeblich sind in diesem Fall die Wärmeleitfähigkeit (k) und die spezifische Wärmekapazität (C). Eine hohe Wärmeleitfähigkeit bedeutet eine schnelle Wärmeübertragung durch ein Material. Eine hohe spezifische Wärmekapazität besagt, dass das Material viel absorbierte Energie benötigt, um seine Temperatur zu erhöhen. Tabelle 2 listet die Wärmeleitfähigkeiten und spezifischen Wärmekapazitäten für verschiedene Tiegelzusammensetzungen auf.
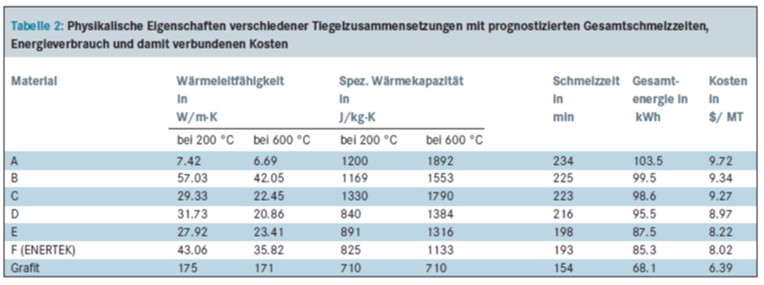
Bei Material A ist die Wärmeleitfähigkeit niedrig und die spezifische Wärmekapazität hoch, was zu der längsten Schmelzzeit des Aluminiums und damit zu den höchsten Energiekosten führt. Material B hat die höchste Gesamtwärmeleitfähigkeit, aber auch eine sehr hohe spezifische Wärmekapazität; daher war die Schmelzzeit nur neun Minuten kürzer als die von Material A. Durch F&E-Arbeiten zur Optimierung dieser Eigenschaften und zur Maximierung der Effizienz wurden die Schmelzzeiten für die Materialien C, D und E reduziert. Schließlich wurde Material F entwickelt, ein Material mit hoher Wärmeleitfähigkeit bei gleichzeitig niedriger spezifischer Wärmekapazität. Wurden diese Eigenschaften in das thermische Modell eingegeben, prognostizierten sie eine Verbesserung der Heizeffizienz um 19,2 %, eine Reduzierung der Schmelzzeit um 41 min und eine Energiekosteneinsparung von 8,02 $ / t.
Einflussfaktor Geometrie
Neben den Materialeigenschaften können geometrische Merkmale eines Tiegels, insbesondere Form und Größe, einen großen Einfluss auf die Energieeffizienz haben. Bild 3 vergleicht Simulationen von zwei verschiedenen Tiegelkonfigurationen. Durch die Änderung der Tiegelgeometrie und die erneute Durchführung von 2-D-Schmelzzeitsimulationen wird deutlich, dass eine Vergrößerung des Tiegels einen wesentlichen Einfluss hat.
Wie bereits erwähnt, führte allein der Wechsel zu einem effizienteren Tiegelmaterial (von E nach F) zu einer Senkung der Netto-Energiekosten. Bei Anwendung auf den kleinen 181 kg-Tiegel liegt die Verbesserung bei lediglich 2,4 % / MT. Bei einer Erhöhung der Tiegelgröße auf das 4-fache sinken die Energiekosten pro MT geschmolzenem Aluminium jedoch deutlich von 8,02 $ auf 3,23 $, was einer Reduzierung von 61 % entspricht. Mit der Volumenzunahme ändert sich das Massenverhältnis von Tiegel zu Aluminium deutlich, sodass mehr Gesamtenergie zum Schmelzen des Aluminiums verbraucht wird als zum Erwärmen des Tiegels. Die absoluten Massen von Feuerfest- und Metallwerkstoffen sind im größeren Tiegel natürlich höher, wodurch sich die Gesamtzeit zum Schmelzen auf 351 Minuten verlängert, aber gleichzeitig steigert sich die Gesamtschmelzleistung von 0,91 kg / min auf 2,32 kg / min, was einer Zunahme von 154 % entspricht. Das Schmelzen der äquivalenten Masse im kleineren Tiegel würde mindestens das 2,5-fache der Zeit in Anspruch nehmen (ohne Nachladen und Schmelzetransfer).
Es ist wahr, dass ein kleinerer Tiegel eine geringere Menge an Aluminium schneller schmelzen kann, sodass je nach Durchsatz einer Gießerei ein kleinerer Tiegel vorteilhaft sein kann, um Energieverluste zu vermeiden. Um große Mengen Aluminium zu schmelzen, ist ein großer Tiegel auf Kosten-per-kg-Basis energieeffizienter, aber es dauert länger, jedoch ist auch Zeit mit Kosten verbunden.
Einflussfaktor thermische Spannung
Wie bei den meisten Bemühungen zur Verbesserung von Eigenschaften gibt es Einschränkungen und Kompromisse. Da Tiegel einem weiten Temperaturbereich ausgesetzt sind und die Änderungsrate (T) stark variieren kann, entstehen beim Gebrauch zwangsläufig thermische Spannungen im Material. Rissbruch und / oder verminderte Lebensdauer sind die Folgen, da feuerfeste Materialien eine begrenzte Duktilität aufweisen. Auf der Suche nach einem verbesserten thermischen Wirkungsgrad durch Materialänderungen könnte die Intensität der Eigenspannungen unwissentlich erhöht werden, sodass der Tiegel die Anwendung nicht übersteht.
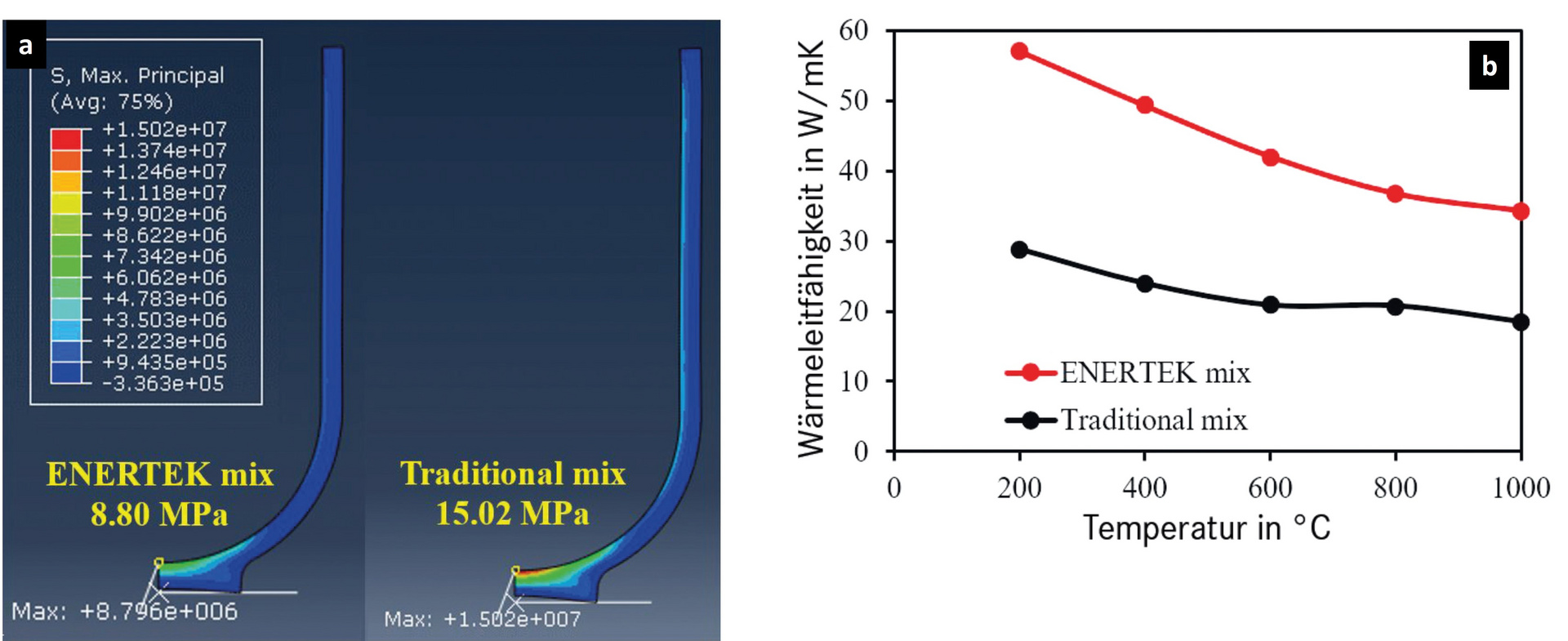
Die hier eingesetzte Software erlaubt als weitere Funktion die Simulation von thermischen Spannungen in Abhängigkeit von Materialeigenschaften, Tiegelgeometrie und Temperatur. Neben den bereits in das Modell eingegebenen, gemessenen mechanischen und physikalischen Eigenschaftsdaten wurden mit einem Datenlogger auch Temperaturprofile aus realen Heizzyklen verschiedener Tiegel erfasst. Mit diesen zusätzlichen Informationen konnten thermische Spannungszustände mit dem Temperatur-Verdrängungsmodell im Programm Abaqus vorhergesagt werden. Bild 3 zeigt ein Beispiel der durch das Computermodell gewonnenen Informationen.
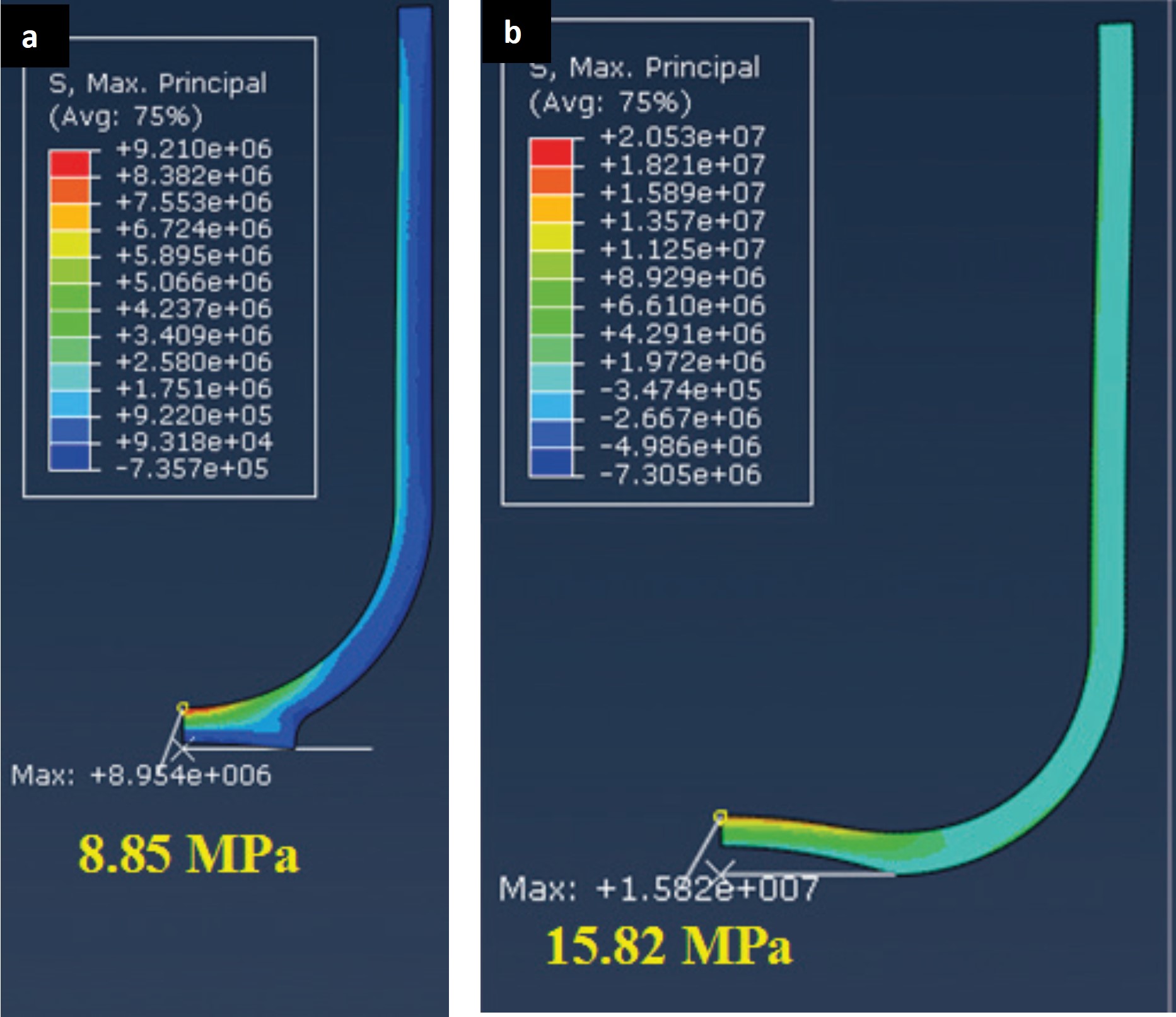
Ein Tiegel aus einem herkömmlichen Feuerfestmaterial (Material E) erfährt beim Erhitzen eine maximale thermische Belastung von 15 MPa. Durch den Wechsel zu einer thermisch effizienten Zusammensetzung (Material F) wird die maximale thermische Belastung deutlich auf 8,8 MPa reduziert. In diesem Fall haben die Bemühungen zur Verbesserung des thermischen Wirkungsgrades auch die thermische Belastung verringert, aber das ist nicht zwingend notwendig. Betrachtet man beispielsweise die Erkenntnis, dass ein größerer Tiegel einen höheren thermischen Wirkungsgrad aufweist, ist das zwar korrekt, aber mit zunehmendem Tiegeldurchmesser steigt auch der Abstand zwischen der niedrigsten Temperaturposition im Tiegelboden (Bild 1b) und den Heizelementen. Dieser längere Leitungsweg führt auch zu einem größeren Temperaturgradienten in der Tiegelwand, der höhere thermische Spannungen erzeugt. Wie in Bild 4 dargestellt, erfährt ein 1055 mm-Durchmesser-Tiegel eine wesentlich höhere thermische Belastung (15,8 MPa) als ein Tiegel mit 655 mm Durchmesser (8,9 MPa). Die hohe Spannung nähert sich der Festigkeit des Tiegelmaterials selbst. Um in dieser Situation einen hohen thermischen Wirkungsgrad großer Tiegel zu erreichen, ohne die Spannungen im Materialdesign zu überschreiten, ist es notwendig, wärmeeffiziente Zusammensetzungen zu verwenden, bei denen eine hohe Wärmeleitfähigkeit dazu beiträgt, Temperaturgradienten und damit thermische Spannungen zu reduzieren.
3-D-Berechnungsmodell
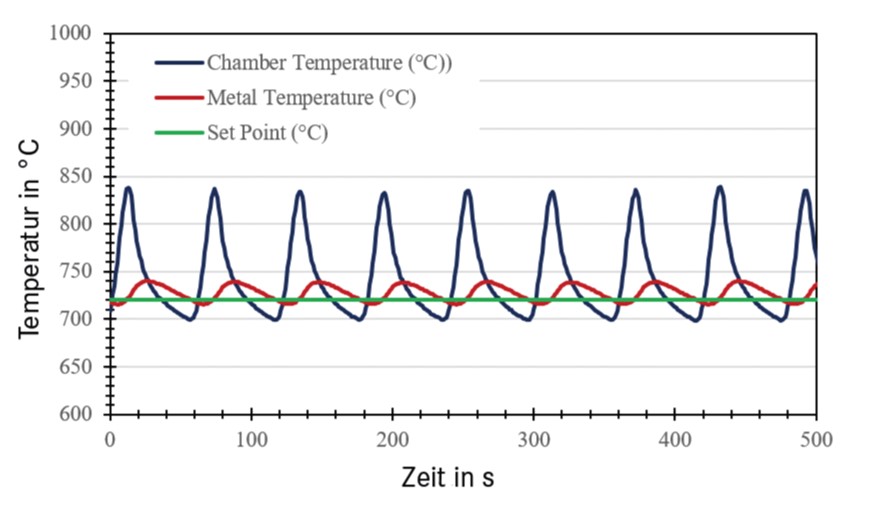
Die zweidimensionale Modellierung ermöglicht die schnelle Berechnung der Energieeffizienz und die Untersuchung verschiedener Effekte der Zusammensetzung, ist jedoch eine starke Vereinfachung eines wesentlich komplizierteren Systems, bei der mehrere wichtige Merkmale und Verhaltensweisen eines tatsächlichen Tiegelofens vernachlässigt werden. Die Konfiguration und die Position der Elektroofen-Heizelemente sind im 2-D-Modell nicht genau definiert, denn ein konstanter Oberflächenwärmestrom ist nicht sehr realistisch. Diese Art von Genauigkeit ist sehr schwierig zu erreichen, da die meisten Tiegelöfen um einen Temperatursollwert herum arbeiten, der einem Thermostat ähnelt. Somit ist der Wärmestrom, der von der Tiegelaußenseite kommt, zyklischer, wobei hohe und niedrige Temperaturen den Sollwert begrenzen (Bild 5).
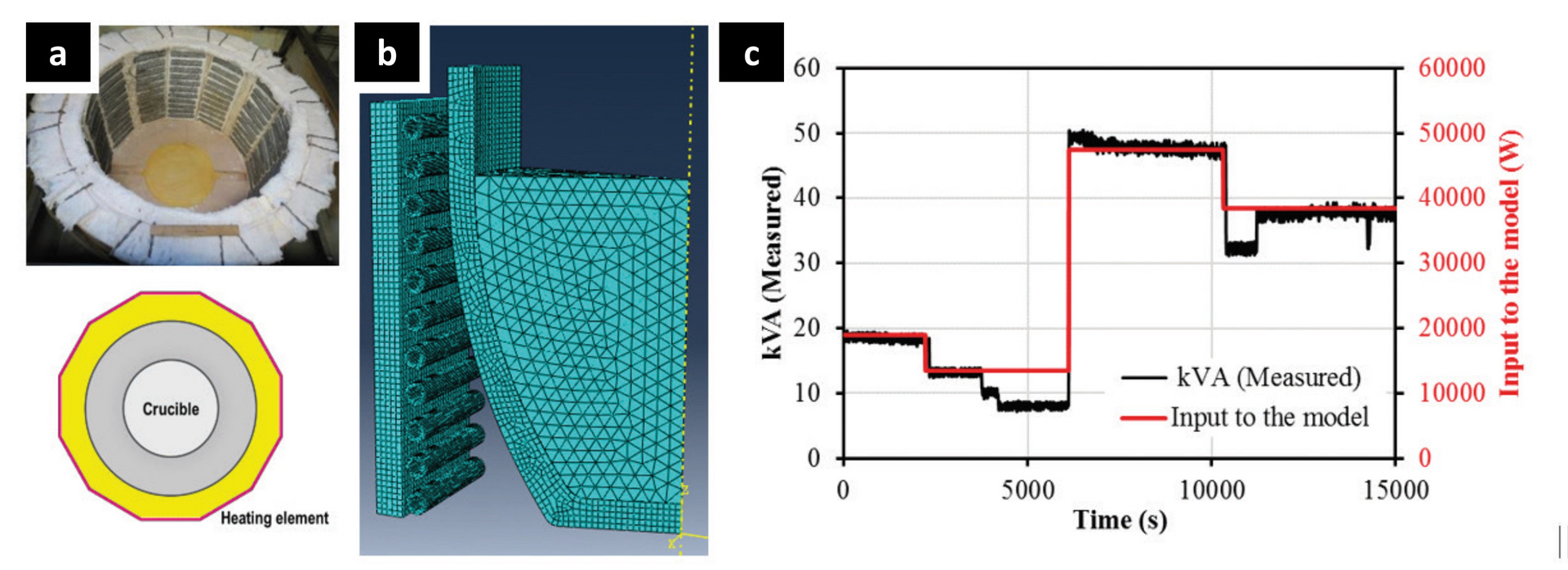
Darüber hinaus ist die Wärmequelle kein Kontinuum, das um den Tiegel herum existiert, sondern ist eher mit Elementblöcken verschiedener Größe und Lage im Ofen zu vergleichen. Um dieses besser zu simulieren, wurde ein verbessertes dreidimensionales Modell konstruiert, basierend auf einem typischen elektrischen Widerstandsofen, bei dem zwölf Heizplatten, die um einen Tiegel herum verteilt sind (Bild 6a). Da die Symmetrie im Ofen noch vorhanden ist, wurde ein 30-Grad-Segment modelliert (Bild 6b), wobei die Abmessungen auf einen tatsächlichen Ofen skaliert wurden, unter Berücksichtigung von Tiegel, Aluminium, Heizelementen und Isolierung. Wie bereits erwähnt, ist der Wärmestrom von den Elementen nicht konstant. Bild 6c (schwarze Linie) zeigt die tatsächliche Leistungsaufnahme des Ofens, gemessen mit einem Datenlogger. Unter Berücksichtigung des Leistungsfaktors wurde die Eingabe in das Modell berechnet (rote Linie), um den tatsächlichen Fall genau zu simulieren. Die Energie wurde als Wärmeströmung in 11 Reihen von Rohrelementen eingebracht.
Sechs verschiedene Wärmeübertragungsszenarien wurden für das Modell berücksichtigt:
- Wärmeströmung, die in Heizelemente eingeleitet und in Strahlung umgewandelt wird,
- Strahlungswärme von Heizelementen, die auf die Tiegelaußenseite ragen,
- Wärmeübertragung zwischen Heizelementen und Blockisolierung.
- Wärmeübertragung zwischen Tiegel und Aluminium.
- Strahlungswärmeübertragung zwischen Isolierung und Außenseite des Tiegels.
- Strahlungswärmeverluste von der Schmelzoberfläche und der Oberseite des Tiegels.
Bild 7 zeigt Visualisierungen des Modells mit Farben, die die Komponententemperaturen (rot >> blau) bei 1 Stunde bzw. 2 Stunden darstellen. In dieser Zeit erreichen die Heizelemente sehr hohe Temperaturen, insbesondere unten und an den Elementkanten, da in diesen Bereichen die Übertragungsraten der Strahlungswärme durch den vergrößerten Abstand zum Tiegel reduziert sind.
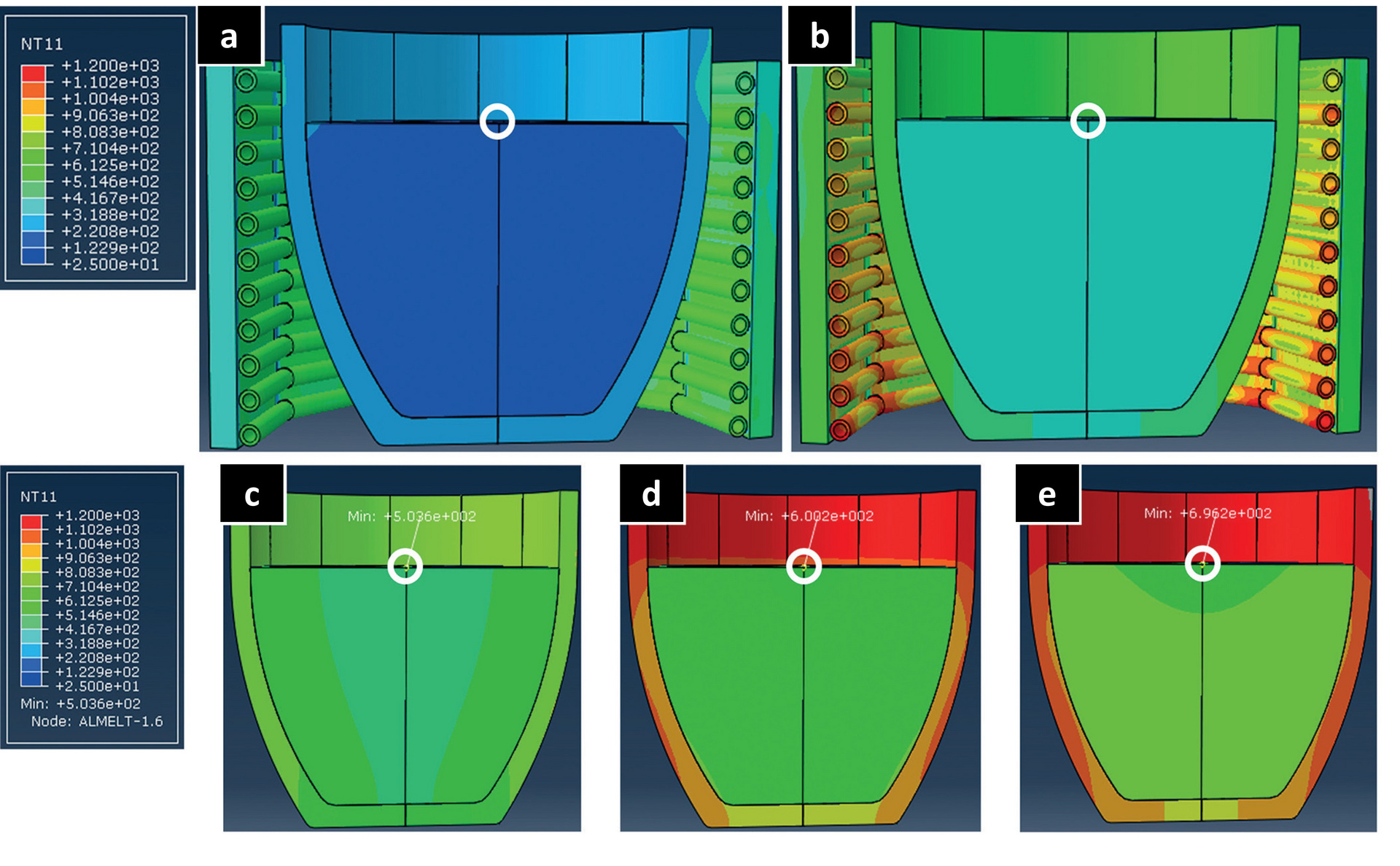
Wie beim zweidimensionalen Modell befindet sich ein temperaturabhängiges Minimum im unteren Zentrum des Tiegels, wobei die Differenz bis zu 300 °C betragen kann. Die Bilder 7c)-e) zeigen ähnliche Temperaturprofile, während das Aluminium (kälteste Stelle) bei 500 °C, 600 °C und 700 °C liegt. Um weitere Aspekte der Tiegelgeometrie in Bezug auf die Schmelzzeit zu untersuchen, wurde für folgende Simulationen das 3-D-Modell eingesetzt. Die Tiegel wurden aus dem hocheffizienten feuerfesten Material F modelliert und anschließend deren Energieverbrauch und theoretischer Wirkungsgrad auf Grundlage der geometrischen Designänderungen berechnet und verglichen. Die erste Geometrie war eine Standard-Tiegelkonstruktion, die nachfolgenden Modelle waren zwar von ähnlicher Form, hatten aber immer dünnere Wandquerschnitte (größere Innendurchmesser). Bild 8 zeigt die niedrigste Temperaturposition in der Schmelze (Kreis in Bild 7) für beide Tiegel in Abhängigkeit von der Zeit. Bild 8b listet die vorhergesagten Eigenschaften beider Tiegel auf. „Effizienz“ ist das prozentuale Verhältnis der Energie, die zum Erwärmen und Schmelzen des Metalls verwendet wird, zur gesamten aufgewendeten Energie.
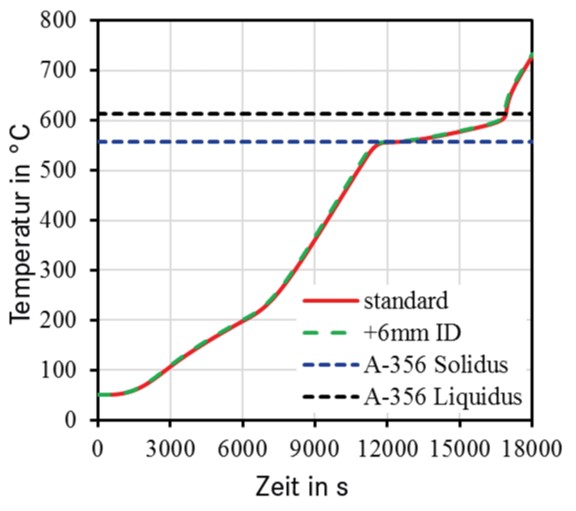
Bild 8 b) ENERTEK mix
| Tiegelmasse in kg | 173 | 157 | 132 | 111 |
| Masse an Al in kg | 353 | 366 | 379 | 403 |
| Schmelzzeit in min | 282 | 280 | 279 | 279 |
| Schmelzrate in kg/min | 1.25 | 1.30 | 1.36 | 1.44 |
| Energieverbrauch in kJ/kg | 1461 | 1400 | 1341 | 1264 |
| Effizienz in % | 65.8 | 68.7 | 71.6 | 72.4 |
Änderung der Tiegeldimensionen einen bedeutenden Einfluss auf die Reduzierung der Masse des Tiegels hat, während die Kapazität des Aluminiums (capacity) zunimmt. Obwohl sich die Schmelzzeit kaum ändert, reduziert sich der Gesamtenergieverbrauch pro kg Aluminium. Für dieses System wird die maximale Schmelzleistung um 15 % von 1,25 auf 1,44 kg / min erhöht. Bei gleichem Energieaufwand des Ofens wird mehr davon auf das Metall gerichtet, da die geringere feuerfeste Masse es absorbiert. Dadurch steigt der Wirkungsgrad von 65,8 % auf 72,4 %. Langfristig kann dies zu erheblichen Einsparungen führen. Es ist zu beachten, dass bei der gleichen Simulation mit Daten aus einem herkömmlichen Tiegelmaterial ein ähnlicher Trend zu beobachten wäre, wenn auch in geringerem Maße als bei dem höher effizienten Tiegelmaterial.
Experimentelle Validierung
Aus den Simulationen geht hervor, dass durch die Verwendung eines thermisch effizienten Tiegelmaterials in Verbindung mit einem Tiegeldesign geringerer Masse und größerer Kapazität, das Schmelzen von Aluminium energiebewusster gestaltet werden kann. Der nächste logische Schritt war die Validierung der Simulationsergebnisse. Für einen speziellen Versuch wurde ein Tiegel aus der Feuerfestzusammensetzung F, mit reduzierter Masse und erhöhter Kapazität in einer US-Gießerei hergestellt. Die Anwendung erfolgte im manuellen Sandguss aus zwei nahezu identischen elektrischen Widerstandsöfen. Dabei wurde immer ein Ofen gehalten, während der andere zum Gießen verwendet wurde. Optimal für die Versuche war, dass beide Öfen von den gleichen Betreibern für den gleichen Betrieb genutzt wurden und so unkontrollierte Variablen in einem industriellen Umfeld minimiert werden konnten. Zusätzlich wurden beide Öfen nur in einer Schicht (8 Stunden/Tag) betrieben und dann für den Rest der Zeit stillgelegt, sodass es möglich war, den Energieverbrauch bei vielen verschiedenen Betriebsarten des Ofens zu erfassen.
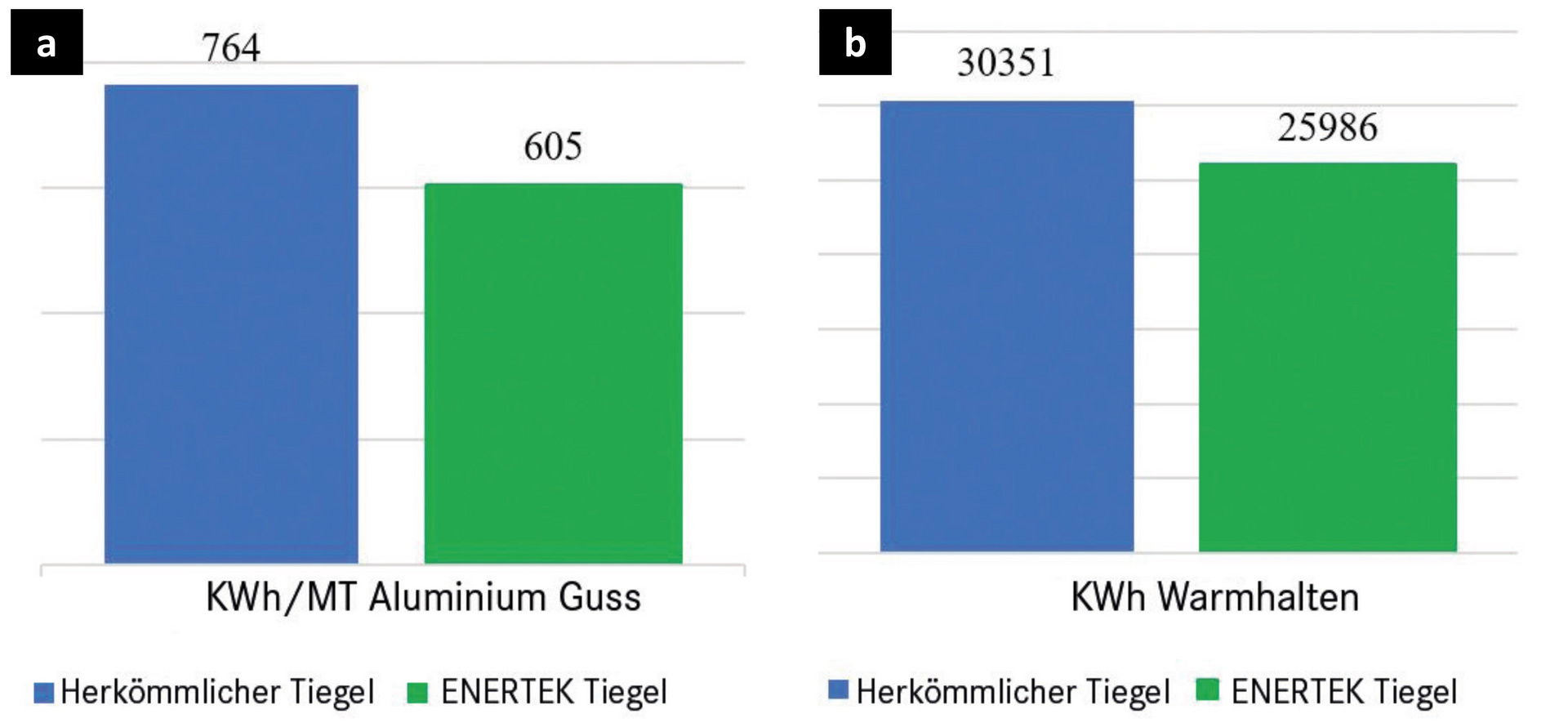
Der Durchsatz des Ofens wurde mit einem kundenspezifischen Tiegel-Energie-/ Durchsatzmonitor genau gemessen, um den Energieverbrauch ständig zu erfassen und die Menge des Metallgusses pro Tag zu verfolgen. Dies ermöglichte eine Normalisierung der Energieergebnisse auf die Menge des gegossenen Aluminiums. Basierend auf einem sechsmonatigen Experiment, bei dem ein Standard-Wettbewerbst i e gel mit einem energieeffizienten Tiegel verglichen wurde, lag die Energieeinsparung beim Gießen in der Größenordnung von 20 % zugunsten des energieeffizienten Tiegels (764 kWh/MT vs. 605 kWh/MT). Gleichzeitig wurde der Gesamtenergieverbrauch um 14 % reduziert (von 30,4 MWh auf 26,0 MWh). Ausgehend von dieser Studie wird geschätzt, dass für einen einzelnen Ofen im Dauerbetrieb das jährliche Energieeinsparpotenzial bis zu 26 MWh oder 2500 $ betragen könnte (ca. 0,08 $ / kWh). Dies bedeutet auch eine Reduzierung der CO2-Emissionen um 16 573 kg pro Ofen und Jahr. In einer Gießerei, die viele Öfen nutzt, könnten die Gesamteinsparungen recht hoch sein.
Zusammenfassung und Schlussfolgerungen
Mit herkömmlichen Bewertungsmethoden, unkontrollierten Feldversuchen oder einfachen Energievergleichen hat sich der Wechsel zu einem energieeffizienten Tiegel als sehr schwierig erwiesen. Fast immer werden die Vorteile durch andere, praxisbezogene Variablen in der Gießerei verdeckt, die die Anlageneffizienz beeinträchtigen. Die Gießerei sollte diese Probleme zunächst beseitigen oder verringern, oft ist es etwas Einfaches wie der Austausch einer beschädigten Isolierung oder den Ofendeckel geschlossen zu halten. Die Vorteile eines Energiespartiegels würden deutlicher zum Tragen kommen. Mit der theoretischen Modellierung ist es möglich, diese Variablen aus der Gleichung zu eliminieren. Damit können Unterschiede in der Energieeffizienz abgeschätzt werden, die direkt durch Änderungen an der Tiegelgeometrie und -zusammensetzung beeinflusst werden. Außerdem können Erkenntnisse darüber gewonnen werden, bis zu welchen Grenzen diese Merkmale geändert werden können, um Energiesparinitiativen zu unterstützen. Es ist wichtig zu beachten, wie sich Änderungen der Zusammensetzung und/oder der Geometrie auf den Spannungszustand des Tiegels auswirken, insbesondere in Abhängigkeit von der Temperatur. Diese Bedingungen können mit einer geringen Menge an Zusatzinformationen in einem Computermodell simuliert werden. Mit der Fähigkeit, die Eigenschaften und das thermische Verhalten von Tiegeln in einem bisher noch relativ unerforschten Maße zu verstehen, wurden neue Materialien entwickelt, die nicht nur theoretisch vielversprechend waren, sondern auch deutliche Verbesserungen zeigten, wenn sie auf einen tatsächlichen Tiegel in einem realen Gießereibetrieb unter genauer Überwachung angewendet wurden. Die gesammelten Messdaten konnten die Ergebnisse aus den Computermodellen validieren.
Die Extrapolation dieser Leistung auf den gesamten Betrieb einer Gießerei verspricht große Auswirkungen in Bezug auf erhöhte Energieeinsparungen, die Minimierung des CO2-Ausstoßes und die Senkung der Gesamtbetriebskosten. Diese Konzepte werden von den Gießereibesitzern und -managern ständig geprüft; mit Hilfe dieser und anderer Bewertungsinstrumente können sie beginnen zu verstehen, dass etwas so Bescheidenes wie ein Tiegel einen erheblichen Einfluss auf ihr Ergebnis haben kann.
Brian Pinto und Wenwu Shi, Foseco NAFTA und Steffen Heumann, European Product Manager Crucibles / Non Ferrous.
Literatur:
[1] K. Salonitis, B. Zeng, H.A. Mehrabi, M. Jolly, Procedia CIRP 40, 24 (2016).
[2] J.Y, Kwon, W. Choate, R. Naranjo. „Advanced Melting Technologies: Energy Saving Concepts and Opportunities for the Metal Casting Industry.“ US Department of Energy, Metal Casting Portfolio 7 (2005).
[3] P.Rohdin, P.Thollander, P. Solding, Energy Policy 35, 672 (2007).
[4] P. Thollander, S. Backlunk, A. Trianni, E. Cagno, Appl. Energy 111, 636 (2013).
[5] Schifo, J. F., and J. T. Radia. „Theoretical/ best practice energy use in metalcasting operations.“US Department of Energy Industrial Technologies Program, Report (2004).
[6] M.R. Jolly, K. Salonitis, F. Charnley, P. Ball, H. Mehrabi, E. Pagone. Light Metals, ed. A.P. Ratvik (New York, NY: Springer, 2017), p. 917.
[7] T.E. Norgate, S. Jahanshahi, W. J. Rankin, J. Cleaner Prod. 15, 838 (2007).
[8] R.M. Torielli, R.A. Abrahams, R.W. Smillie, R.C. Voigt, China Foundry 8, 74 (2011)
[9] S. Dalquist, T. Gutowski, Proceeding of IMECE. 62599, (2004).
[10] S. Fore, C. T. Mbohwa. J. eng. design technol. 8, 314 (2010).
[11] Brown, John. Foseco non-ferrous foundryman‘s handbook, 11th ed. (Woburn, MA: Butterworth-Heinemann, 1999).
[12] D.M. Stefanescu, ASM Handbook Vol. 15 Casting, (ASM International, 2008).
[13] A.O. Nieckele, M.F. Naccache, M.S.P. Gomes. Appl. Therm. Eng. 31, 841 (2011).
[14] R.T. Bui, R. Ouellet. Metall. Mater. Trans. B 21, 487 (1990).
[15] Trinks, Willibald. Industrial furnaces. Vol. 1. (John Wiley & Sons, 2004).
[16] K. Pericleous, V. Bojarevics, G. Djambazov, R.A. Harding, M. Wickins, Appl. Math. Model. 30, 1262 (2006).





