Gusseisen mit Kugelgraphit
Mechanische und physikalische Eigenschaften
Inhalt dieser Seite
Eigenschaften bei Raumtemperatur
Die Bezeichnung „Gusseisen mit Kugelgraphit“ leitet sich vom Vorliegen kugelförmiger Graphitausscheidungen in diesen Werkstoffen ab (Bild 128).
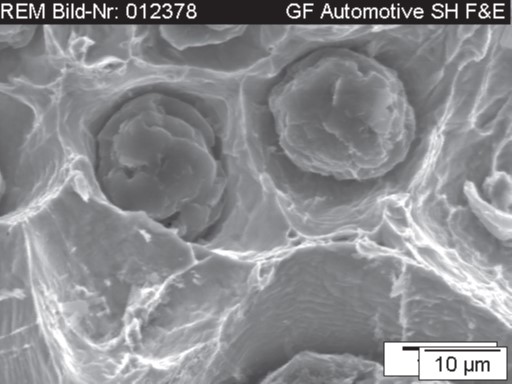
Anders als bei Gusseisen mit Lamellengraphit, bei dem wegen der ausgeprägten Kerbwirkung des Graphits die mechanischen Eigenschaften durch dessen Menge, Verteilung und Form dominiert werden, hat bei Gusseisen mit Kugelgraphit die Ausbildung der metallischen Matrix entscheidenden Einfluss. Die Struktur der metallischen Matrix ist bei den konventionellen, in DIN EN 1563 genormten Werkstoffen ferritisch, perlitisch oder eine Mischform dieser beiden Grundgefüge (siehe Bild 13).

Zur Gruppe der Gusseisenwerkstoffe mit Kugelgraphit gehören darüber hinaus auch die in DIN EN 1564 genormten ausstenitisch-ferritischen Gusseisen mit Kugelgraphit, auch als ADI bekannt, sowie die in DIN EN 13835 beschriebenen austenitischen Gusseisen mit Kugelgraphit.
Je nach Matrixstruktur werden bei den nach DIN EN 1563 definierten konventionellen un- und niedrig legierten Werkstoffen, die Festigkeitsstufen EN-GJS-350-22 bis EN-GJS-900-2 erreicht. Das ferritische Grundgefüge besteht aus kubisch raumzentriertem α-Eisen. Diese Phase ist sehr zäh und duktil, allerdings durch begrenzte Festigkeit und geringe Härte charakterisiert. Perlit ist eine zeilige Gefügestruktur, die aus abwechselnden Schichten von Ferrit und Zementit (Fe3C) besteht. Diese Phase ist im Gegensatz zum Ferrit sehr fest und durch eine hohe Härte und einen hohen Verschleißwiderstand gekennzeichnet. Allerdings ist die Verformbarkeit gering. So bildet Ferrit die Basis der duktilen, weniger festen Gusseisensorten, während die höherfesten Sorten überwiegend perlitisch sind. Durch Kombination unterschiedlicher Mengenanteile beider Gefüge entstehen die verschiedenen Übergangsqualitäten. Die Werkstoffsorten EN-GJS-800-2 und EN-GJS-900-2 weisen zumeist ein Vergütungsgefüge auf. So decken bereits un- und niedriglegierte Gusseisensorten mit Kugelgraphit eine große Bandbreite von Eigenschaften ab.
Anders als bei anderen Werkstoffgruppen ist die chemische Zusammensetzung von un- und niedrig legiertem Gusseisen mit Kugelgraphit nicht durch die Norm vorgeschrieben. Vielmehr erfolgt die Werkstoffdefinition über die mechanischen Eigenschaften, was sich auch in der Werkstoffbezeichnung widerspiegelt. Während über die Bezeichnung GJS die Klassifizierung der Graphitstruktur als Gusseisen mit Kugelgraphit erfolgt, geben die Ziffern im Kurzzeichen die Mindestzugfestigkeit in N/mm2 (MPa) sowie den Mindestwert für die Bruchdehnung in getrennt gegossenen Proben an.
Die überwiegend ferritische Sorte ENGJS-400-18 enthält keine oder nur geringfügige Anteile an Perlit. Sie besitzt bei guter Festigkeit eine hohe Bruchdehnung und ist wegen ihrer niedrigen Härte hervorragend zu bearbeiten. Für den Einsatz bei niedrigen oder stark schwankenden Temperaturen haben sich die ferritischen Sorten mit gewährleisteter Kerbschlagarbeit EN-GJS-350-22-RT oder EN-GJS-350-22-LT beziehungsweise EN-GJS-400-18-RT oder EN-GJS-400-18-LT ausgezeichnet bewährt. Der Zusatz RT bedeutet, dass die Kerbschlagarbeit für Raumtemperatur gewährleistet ist, während bei dem Zusatz LT (= low temperature) die Kerbschlagarbeit für eine Prüfung bei tiefen Temperaturen angegeben ist.
Für höhere Anforderungen an die Belastbarkeit kann auf die Sorte EN-GJS-450-10 verwiesen werden, die bei immer noch sehr hoher Duktilität eine höhere Festigkeit aufweist. Für noch höhere Festigkeitsanforderungen werden EN-GJS-500-7 und EN-GJS-600-3 verwendet. Neben einer ausreichenden Zähigkeit bieten diese Werkstoffsorten die Gewähr für eine wirtschaftliche spanende Bearbeitung. Darüber hinaus können sie gut randschichtgehärtet werden.
Die Sorten EN-GJS-700-2, EN-GJS-800-2 und EN-GJS-900-2 werden mit Erfolg anstelle von Schmiedestählen gleicher Festigkeitsstufe eingesetzt. Häufig ist der Grund für den Einsatz dieser Sorten der Verschleißwiderstand, der beispielsweise durch lokales Härten in besonders hoch belasteten Bereichen nochmals gesteigert werden kann. Trotz der hohen Festigkeit dieser Werkstoffe sind gute Voraussetzungen für die spanende Bearbeitung gegeben.
Für duktile Rohre (Rohre aus ferritischem Gusseisen mit Kugelgraphit) für Wasserund Gasleitungen sind nach DIN EN 545 folgende mechanische Eigenschaften festgelegt:
- Mindestzugfestigkeit: 420 N/mm²;
- Mindestbruchdehnung bei Nenndurchmesser 40 bis 1000 mm: 10 %;
- Mindestbruchdehnung bei Nenndurchmesser 1100 bis 2000 mm: 7 %.
Bei den nach DIN EN 1564 genormten austenitisch-ferritischen Gusseisensorten, die in der Literatur häufig auch als ADI (Austempered Ductile Iron) bezeichnet werden, wird durch eine nachgeschaltete, separate Wärmebehandlung eine spezielle Mikrostruktur eingestellt. Diese besteht aus lattenförmigem Ferrit, der in einer an Kohlenstoff übersättigten austenitischen Matrix vorliegt. Daher wird diese Struktur in der neueren Literatur auch als „Ausferrit“ bezeichnet. In älteren Veröffentlichungen wurde diese Struktur häufig als „zwischenstufenvergütetes“ oder „bainitisches“ Gusseisen bezeichnet. Anders als bei der bainitischen Struktur von Stahl liegen jedoch bei einem austenitisch-ferritischen Gefüge keine fein verteilten Carbide vor, so dass diese Bezeichnung streng genommen nicht ganz korrekt ist. In DIN EN 1564 sind vier Sorten genormt, die zu der Werkstoffgruppe gehören. Die wichtigsten Eigenschaften dieser Gusseisensorten sind ebenfalls mit in Tabelle 9 aufgeführt.
Tabelle 9: Gewährleistete Mindestwerte nach DIN EN 1563 und DIN EN 1564 und weitere Anhaltswerte für die mechanischen und physikalischen Eigenschaften von Gusseisen mit Kugelgraphit
| Eigenschaften | Werkstoffkurzzeichen Werkstoffnummer EN-... | |||||
| GJS-350-22- LT JS1015 | GJS-350-22U- LT JS1019 | GJS-350-22- RT JS1014 | GJS-350-22U- RT JS1029 | GJS-350- 22 JS1010 | GJS-350-22U JS1032 | |
| Gefüge | Ferrit | Ferrit | Ferrit | Ferrit | Ferrit | Ferrit |
| Zugfestigkeit Rm1 [N/mm²] | 350 | 320 | 350 | |||
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 350 330 320 | 350 330 320 | 350 330 320 | |||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 220 | 220 | 220 | |||
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 220 210 200 | 220 210 200 | 220 210 200 | |||
| Bruchdehnung A51 [%] | 22 | 22 | 22 | |||
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 22 18 15 | 22 18 15 | 22 18 15 | |||
| Brucheinschnürung Z [%] | 20-35 | |||||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | 17 14 | |||||
| Kerbschlagarbeit Av -40°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | 12 9 | |||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | 17 14 14 12 | |||||
| Kerbschlagarbeit Av -40 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | 12 9 | |||||
| Kerbschlagarbeit Av -40 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | 10 7 | |||||
| Härte HB3013 | < 160 | |||||
| Elastizitätsmodul E014 [kN/mm²] | 169 | |||||
| Schubmodul G [kN/mm²] | ~ 68 | |||||
| Querkontraktionszahl ν 14 | 0,275 | |||||
| Torsionsfestigkeit τt14 [N/mm²] | 315 | |||||
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | ||||||
| Scherfestigkeit τaB14 [N/mm²] | 315 | |||||
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | 114 | |||||
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | 114 | |||||
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | +/- 100 | |||||
| Biegewechselfestigkeit σbW6 [N/mm²] | +/- 185 | |||||
| Bruchzähigkeit Kic14 [N/mm² m] | 31 | |||||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C | 200 170 140 | |||||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 36,2 | |||||
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | 515 | |||||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 12,5 | |||||
| Dichte 14 [g/dm³] | 7,1 | |||||
| maximale Permeabilität 14 [μH/m] | 2136 | |||||
| Hystereseverlust (b = 11 T) 14 [J/m³] | 600 | |||||
| spezifischer elektrischer Widerstand 14 [μO*m] | 0,5 | |||||
| Eigenschaften | |||||
| GJS-400-18-LT JS1025 | GJS-400-18U-LT JS1049 | GJS-400-18-RT JS1024 | GJS-400-18U-RT JS1059 | GJS-400-18 JS1020 | |
| Gefüge | Ferrit | Ferrit | Ferrit | Ferrit | Ferrit |
| Zugfestigkeit Rm1 [N/mm²] | 400 | 400 | 400 | ||
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 400 390 370 | 400 390 370 | |||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 240 | 250 | 250 | ||
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 240 230 220 | 250 250 240 | |||
| Bruchdehnung A51 [%] | 18 | 18 | 18 | ||
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 18 15 12 | 18 15 12 | |||
| Brucheinschnürung Z [%] | 17-32 | ||||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | 14 11 | ||||
| Kerbschlagarbeit Av -40°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | 12 9 | ||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | 14 11 12 9 | ||||
| Kerbschlagarbeit Av -40 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | 12 9 | ||||
| Kerbschlagarbeit Av -40 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | 10 7 | ||||
| Härte HB3013 | 130 - 175 | ||||
| Elastizitätsmodul E014 [kN/mm²] | 169 | ||||
| Schubmodul G [kN/mm²] | ~ 68 | ||||
| Querkontraktionszahl ν 14 | 0,275 | ||||
| Druckfestigkeit σdb 14 [N/mm²] | 700 | ||||
| 0,2%-Stauchgrenze σd0,2 [N/mm²] | |||||
| Torsionsfestigkeit τt14 [N/mm²] | 360 | ||||
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | 190 | ||||
| Scherfestigkeit τaB14 [N/mm²] | 360 | ||||
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | 195 | ||||
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | 122 | ||||
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | +/- 110 | ||||
| Biegewechselfestigkeit σbW6 [N/mm²] | +/- 20’0 | ||||
| Biegewechselfestigkeit σbW (Kt = 1,17) 5 [N/mm²] | |||||
| Biegeschwellfestigkeit σbS (Kt = 1,1) 5 [N/mm²] | |||||
| Torsionswechselfestigkeit τtW (Kt = 1,0) 7 [N/mm²] | |||||
| Bruchzähigkeit Kic14 [N/mm² m] | 30 | ||||
| Grübchendauerfestigkeit σ H lim8 [N/mm²] | |||||
| Zahnfußfestigkeit σF lim8 [N/mm²] | |||||
| Statische Zahnfußfestigkeit σVB9 [N/mm²] | |||||
| Laufradpressung pzul10[N/mm²] | |||||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C Wanddicke bis 60 - 200 mm: 150 °C 250 °C 350 °C | 230 200 160 210 180 140 | ||||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 36,2 | ||||
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | 515 | ||||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 12,5 | ||||
| Dichte 14 [g/dm³] | 7,1 | ||||
| maximale Permeabilität 14 [μH/m] | 2136 | ||||
| Hystereseverlust (b = 11 T) 14 [J/m³] | 600 | ||||
| spezifischer elektrischer Widerstand 14 [μO*m] | 0,5 |
| Eigenschaften | |||||
| GJS-400-18U JS1062 | GJS-400-15 JS1030 | GJS-450-10 JS1040 | GJS-450-10U JS1032 | GJS-500-7 JS1050 | |
| Gefüge | Ferrit | Ferrit | Ferrit/Perlit | Ferrit/Perlit | Ferrit/Perlit |
| Zugfestigkeit Rm1 [N/mm²] | 400 | 450 | 500 | ||
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 400 390 370 | 450 z. v. z. v. | |||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 250 | 310 | 320 | ||
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 250 250 240 | 310 z. v. z. v. | |||
| Bruchdehnung A51 [%] | 15 | 10 | 7 | ||
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 18 15 12 | 10 z. v. z. v. | |||
| Brucheinschnürung Z [%] | 15 - 30 | 7 - 20 | |||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Härte HB3013 | 135 - 180 | 160 - 210 | 170 - 230 | ||
| Elastizitätsmodul E014 [kN/mm²] | 169 | 169 | |||
| Schubmodul G [kN/mm²] | ~ 68 | ~ 68 | |||
| Querkontraktionszahl ν 14 | 0,275 | 0,275 | |||
| Druckfestigkeit σdb 14 [N/mm²] | 700 | 800 | |||
| 0,2%-Stauchgrenze σd0,2 [N/mm²] | 350 | ||||
| Torsionsfestigkeit τt14 [N/mm²] | 405 | 450 | |||
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | 230 | ||||
| Scherfestigkeit τaB14 [N/mm²] | 405 | 450 | |||
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | 210 128 | 224 134 | |||
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | |||||
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | +/- 110 | +/- 150 | |||
| Zug-Druck-Wechselfestigkeit σzdW (Kt = 1,05) 5 | +/- 218 | ||||
| Biegewechselfestigkeit σbW6 [N/mm²] | +/- 200 | +/- 220 | |||
| Biegewechselfestigkeit σbW (Kt = 1,17) 5 [N/mm²] | +/- 211 | ||||
| Biegeschwellfestigkeit σbS (Kt = 1,1) 5 [N/mm²] | +/- 177 | ||||
| Torsionswechselfestigkeit τtW (Kt = 1,0) 7 [N/mm²] | +/- 200 | ||||
| Bruchzähigkeit Kic14 [N/mm² m] | 23 | 25 | |||
| Grübchendauerfestigkeit σ H lim8 [N/mm²] | 440 | 500 | |||
| Zahnfußfestigkeit σF lim8 [N/mm²] | 175 | 185 | |||
| Statische Zahnfußfestigkeit σVB9 [N/mm²] | 990 | 1290 | |||
| Laufradpressung pzul10[N/mm²] | 3,6 | 4,5 | |||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C Wanddicke bis 60 - 200 mm: 150 °C 250 °C 350 °C | 230 200 160 210 180 150 | 290 250 200 240 200 160 | |||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 36,2 | 35,2 | |||
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | 515 | 515 | |||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 12,5 | 12,5 | |||
| Dichte 14 [g/dm³] | 7,1 | 7,1 | |||
| maximale Permeabilität 14 [μH/m] | 2136 | 1596 | |||
| Hystereseverlust (b = 11 T) 14 [J/m³] | 600 | 1345 | |||
| spezifischer elektrischer Widerstand 14 [μO*m] | 0,5 | 0,51 |
| Eigenschaften | |||||
| GJS-500-7U JS1082 | GJS-600-3 JS1060 | GJS-600-3U JS1092 | GJS-700-2 JS1070 | GJS-700-2U JS1102 | |
| Gefüge | Ferrit/Perlit | Ferrit/Perlit | Ferrit/Perlit | Perlit | Perlit |
| Zugfestigkeit Rm1 [N/mm²] | 600 | 700 | |||
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 500 450 120 | 600 600 550 | 700 700 660 | ||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 370 | 420 | |||
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 320 300 290 | 370 360 340 | 420 400 380 | ||
| Bruchdehnung A51 [%] | 3 | 2 | |||
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 7 7 5 | 3 2 1 | 2 2 1 | ||
| Brucheinschnürung Z [%] | 3 - 8 | 2 - 6 | |||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | |||||
| Härte HB3013 | 190 - 270 | 225 - 305 | |||
| Elastizitätsmodul E014 [kN/mm²] | 174 | 176 | |||
| Schubmodul G [kN/mm²] | ~ 70 | ~ 70 | |||
| Querkontraktionszahl ν 14 | 0,275 | 0,275 | |||
| Druckfestigkeit σdb 14 [N/mm²] | 870 | 1000 | |||
| 0,2%-Stauchgrenze σd0,2 [N/mm²] | 460 | 540 | |||
| Torsionsfestigkeit τt14 [N/mm²] | 540 | 630 | |||
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | 300 | 330 | |||
| Scherfestigkeit τaB14 [N/mm²] | 540 | 630 | |||
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | 248 | 280 | |||
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | |||||
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | +/- 175 | +/- 200 | |||
| Zug-Druck-Wechselfestigkeit σzdW (Kt = 1,05) 5 | +/- 259 | ||||
| Biegewechselfestigkeit σbW6 [N/mm²] | +/- 173 | ||||
| Biegewechselfestigkeit σbW (Kt = 1,17) 5 [N/mm²] | +/- 250 | ||||
| Biegeschwellfestigkeit σbS (Kt = 1,1) 5 [N/mm²] | +/- 259 | +/- 280 | |||
| Torsionswechselfestigkeit τtW (Kt = 1,0) 7 [N/mm²] | +/- 202 | ||||
| Bruchzähigkeit Kic14 [N/mm² m] | +/- 250 | +/- 300 | |||
| Grübchendauerfestigkeit σ H lim8 [N/mm²] | 20 | 15 | |||
| Zahnfußfestigkeit σF lim8 [N/mm²] | 535 | 570 | |||
| Statische Zahnfußfestigkeit σVB9 [N/mm²] | 195 | 210 | |||
| Laufradpressung pzul10[N/mm²] | 1300 | 1320 | |||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C Wanddicke bis 60 - 200 mm: 150 °C 250 °C 350 °C | 5,6 340 300 220 290 260 190 | 6,5 390 350 280 330 300 250 | |||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 32,5 | 31,1 | |||
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | 515 | 515 | |||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 12,5 | 12,5 | |||
| Dichte 14 [g/dm³] | 7,2 | 7,2 | |||
| maximale Permeabilität 14 [μH/m] | 866 | 501 | |||
| Hystereseverlust (b = 11 T) 14 [J/m³] | 2248 | 2700 | |||
| spezifischer elektrischer Widerstand 14 [μO*m] | 0,53 | 0,54 |
| Eigenschaften | ||||
| GJS-800-2 JS1080 | GJS-800-2U JS1112 | GJS-900-2 JS1090 | GJS-900-2U JS1122 | |
| Gefüge | Perlit oder Vergütungsgefüge | Vergütungsgefüge | Vergütungsgefüge | |
| Zugfestigkeit Rm1 [N/mm²] | 800 | 900 | ||
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 800 z. v. z. v. | 900 z. v. z. v. | ||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 480 | 600 | ||
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 480 z. v. z. v. | 600 z. v. z. v. | ||
| Bruchdehnung A51 [%] | 2 | 2 | ||
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | 2 z. v. z. v. | 2 z. v. z. v. | ||
| Brucheinschnürung Z [%] | 2 - 4 | |||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av -20°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Härte HB3013 | 245 - 335 | 270 - 360 | ||
| Elastizitätsmodul E014 [kN/mm²] | 176 | 176 | ||
| Schubmodul G [kN/mm²] | ~ 70 | ~ 70 | ||
| Querkontraktionszahl ν 14 | 0,275 | 0,275 | ||
| Druckfestigkeit σdb 14 [N/mm²] | 1150 | |||
| 0,2%-Stauchgrenze σd0,2 [N/mm²] | 690 | |||
| Torsionsfestigkeit τt14 [N/mm²] | 720 | 810 | ||
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | ||||
| Scherfestigkeit τaB14 [N/mm²] | 720 | 810 | ||
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | +/-304 | +/-317 | ||
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | +/-182 | +/-190 | ||
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | +/-200 | |||
| Zug-Druck-Wechselfestigkeit σzdW (Kt = 1,05) 5 | ||||
| Biegewechselfestigkeit σbW6 [N/mm²] | +/-300 | |||
| Biegewechselfestigkeit σbW (Kt = 1,17) 5 [N/mm²] | +/-262 | |||
| Biegeschwellfestigkeit σbS (Kt = 1,1) 5 [N/mm²] | +/-202 | |||
| Torsionswechselfestigkeit τtW (Kt = 1,0) 7 [N/mm²] | ||||
| Bruchzähigkeit Kic14 [N/mm² m] | 14 | 14 | ||
| Grübchendauerfestigkeit σ H lim8 [N/mm²] | 640 | |||
| Zahnfußfestigkeit σF lim8 [N/mm²] | 225 | |||
| Statische Zahnfußfestigkeit σVB9 [N/mm²] | 1400 | |||
| Laufradpressung pzul10[N/mm²] | ||||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C Wanddicke bis 60 - 200 mm: 150 °C 250 °C 350 °C | ||||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 31,1 | 31,1 | ||
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | 515 | 515 | ||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 12,5 | 12,5 | ||
| Dichte 14 [g/dm³] | 7,2 | 7,2 | ||
| maximale Permeabilität 14 [μH/m] | 501 | 501 | ||
| Hystereseverlust (b = 11 T) 14 [J/m³] | 2700 | 2700 | ||
| spezifischer elektrischer Widerstand 14 [μO*m] | 0,54 | 0,54 | ||
| Eigenschaften | ||||
| GJS-800-8 16 J1100 | GJS-1000-5 16 JS1110 | GJS-1200-2 16 JS1120 | GJS-1400-1 16 JS1130 | |
| Gefüge | Ausferrit und Austenit | |||
| Zugfestigkeit Rm1 [N/mm²] | 800 | 1000 | 1200 | 1400 |
| Zugfestigkeit Rm2 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | ||||
| 0,2%-Dehngrenze Rp0,21 [N/mm²] | 500 | 700 | 850 | 1100 |
| 0,2%-Dehngrenze Rp0,22 [N/mm²] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | ||||
| Bruchdehnung A51 [%] | 8 | 5 | 2 | 1 |
| Bruchdehnung A52 [%] maßgebende Wanddicke: bis 30 mm >30 - 60 mm >60 - 200 mm | ||||
| Brucheinschnürung Z [%] | ||||
| Kerbschlagarbeit Av RT1 [J] Mittelwert aus drei Prüfungen Einzelwert | 10 9 | |||
| Kerbschlagarbeit Av -20°C1 [J] Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av RT2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert Wanddicke > 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Kerbschlagarbeit Av -20 °C2 Wanddicke bis 60 - 200 mm: Mittelwert aus drei Prüfungen Einzelwert | ||||
| Härte HB3013 | 260 - 320 | 300 - 360 | 340 - 440 | 380 - 480 |
| Elastizitätsmodul E014 [kN/mm²] | 170 | 168 | 167 | 165 |
| Schubmodul G [kN/mm²] | 65 | 64 | 63 | 62 |
| Querkontraktionszahl ν 14 | ||||
| Druckfestigkeit σdb 14 [N/mm²] | 1300 | 1600 | 1900 | 2200 |
| 0,2%-Stauchgrenze σd0,2 [N/mm²] | 620 | 770 | 1040 | 1220 |
| Torsionsfestigkeit τt14 [N/mm²] | 720 | 900 | 1080 | 1260 |
| 0,2%-Torsionsgrenze τt0,2 [N/mm²] | 350 | 490 | 590 | 770 |
| Scherfestigkeit τaB14 [N/mm²] | 720 | 900 | 1080 | 1260 |
| Umlaufbiegewechselfestigkeit ungekerbt, Probendmr. 10,6 mm 14 [N/mm²] | 375 | 425 | 450 | 375 |
| Umlaufbiegewechselfestigkeit [N/mm²] gekerbt15, Probendurchmesser 10,6 mm14 | 225 | 260 | 280 | 275 |
| Zug-Druck-WechselfestigkeitσzdW4 [N/mm²] | ||||
| Zug-Druck-Wechselfestigkeit σzdW (Kt = 1,05) 5 | ||||
| Biegewechselfestigkeit σbW6 [N/mm²] | ||||
| Biegewechselfestigkeit σbW (Kt = 1,17) 5 [N/mm²] | ||||
| Biegeschwellfestigkeit σbS (Kt = 1,1) 5 [N/mm²] | ||||
| Torsionswechselfestigkeit τtW (Kt = 1,0) 7 [N/mm²] | ||||
| Bruchzähigkeit Kic14 [N/mm² m] | 62 | 58 | 54 | 50 |
| Grübchendauerfestigkeit σ H lim8 [N/mm²] | ||||
| Zahnfußfestigkeit σF lim8 [N/mm²] | 235 | 310 | 250 | |
| Statische Zahnfußfestigkeit σVB9 [N/mm²] | 1280 | 1940 | 1940 | |
| Laufradpressung pzul10[N/mm²] | ||||
| 0,2-%-Dehngrenze [N/mm²] in Abhängigkeit der Temperatur 11: Wanddicke bis 60 mm: 150 °C 250 °C 350 °C Wanddicke bis 60 - 200 mm: 150 °C 250 °C 350 °C | ||||
| Wärmeleitfähigkeit bei 300 °C 14 [W/K*m] | 22,1 | 21,8 | 21,5 | 21,2 |
| spez. Wärmekapazität 20 - 500 °C14 [J/kg*K] | ||||
| thermischer Längenausdehnungskoeffizient [μm/m*K] 20 - 400 °C 14 | 14,6 | 14,3 | 14,0 | 13,8 |
| Dichte 14 [g/dm³] | 7,1 | 7,1 | 7,1 | 7,1 |
| maximale Permeabilität 14 [μH/m] | ||||
| Hystereseverlust (b = 11 T) 14 [J/m³] | ||||
| spezifischer elektrischer Widerstand 14 [μO*m] | ||||
1 nach DIN EN 1563 gewährleistete Werte für getrennt gegossene Probestücke
2 nach DIN EN 1563 gewährleistete Werte aus angegossenen Probestücken
3 Richter, F.: Giess.-Forsch. 37 (1985) H. 3, S. 97 - 102
4 Hänchen, R.: Dauerfestigkeitsschaubilder für Stahl und Gusseisen. C. Hanser-Verlag München 1964
5 Hück, M, W. Schütz u. H. Walter: ATZ 86 (1984) H. 7/8, S. 325 - 331 und H. 9, S. 385 - 388
6 Gilbert, G. N. J.: BCIRA-Report 1160. Alvechurch, Birmingham 1974
7 Hornung, K., u. A. Rist: Material und Technik 2 (1974) H. 2, S. 63 - 68
8 nach DIN 3990 Teil 5, gültig für Werkstoffqualität MQ
9 Niemann, G., u. H. Winter: Maschinenelement Bd. II, 2. Aufl., Springer-Verlag 1983
10 nach DIN 15 070
11 nach AD-2000-Merkblatt , W 3/2, 2003
12 nach DIN EN 1564 gewährleistete Werte für getrennt gegossene Probestücke
13 in Anlehnung an DIN EN 1563, Einteilung nach Härte (informativ)
14 Richtwerte nach DIN EN 1563, Anhang B (informativ)
15 45°-Spitzkerbe mit r = 0,25 mm
16 austenitisch-ferritische Sorten (ADI) nach DIN EN 1564
17 ADI- The brenchmark engineering material: Sonderdruck der CAIF d. i. Group, 2002
18 Hasse, S.: Duktiles Gusseisen. Schiele & Schön, Berlin 1996 z. v. - mit Gießerei zu vereinbaren
Für ADI-Werkstoffe sind Anhaltswerte für eine Vielzahl von mechanischen und physikalischen Eigenschaften in ISO 17804 zusammengestellt. Zwar weichen die Werkstoffdefinitionen hier leicht von den in DIN EN 1564 festgelegten Sorten ab, dennoch sind dort für den Konstrukteur wichtige Hinweise zu finden. Weiterführende Informationen zu ADI-Werkstoffen sind in [111] zu finden.
Die Entwicklung von Werkstoffen ist bei weitem nicht abgeschlossen, sondern es wird stetig hieran weitergearbeitet, und so gibt es außer den genormten Sorten beim Gusseisen mit Kugelgraphit auch eine Reihe von jüngeren Sonderwerkstoffen, deren garantierte Mindesteigenschaften in bestimmten Bereichen deutlich über die der Standardwerkstoffe hinaus gehen. Das für Fahrwerksteile entwickelte Sibo-Dur [112] gehört ebenso in diese Gruppe wie der für Kugelstangen eingesetzte Werkstoff „GJS-520-12“ oder der im Getriebebau verwendete Sonderwerkstoff „GJS-620-7“.
Gusseisen mit Kugelgraphit kann nicht nur im Formguss, sondern auch im Strangguss vergossen werden (Bild 133). Für den Strangguss existiert derzeit keine eigene Norm. Generell erfolgt die Bezeichnung der Sorten nach DIN EN 1560 analog zu denen für den Sandguss, also nach der Zugfestigkeit und der Bruchdehnung oder nach der Brinellhärte. Anders als beim Sandguss werden die Werkstoffeigenschaften jedoch nicht an einem separat gegossenen Probestab ermittelt, sondern immer an Proben, die an genau festgelegten Stellen aus dem Strang entnommenen wurden, was in der Werkstoffbezeichnung durch den Zusatz C zum Ausdruck kommt. Wie auch beim Sandguss sind die mechanischen Eigenschaften von Stranggussprodukten aus Gusseisen mit Kugelgraphit wandstärkenabhängig. Werte sind in [34] enthalten.

Verfahrensbedingt ergeben sich jedoch auf Grund der hohen Abkühlrate andere mechanische Eigenschaften als im Sandguss. So werden im Gusszustand ohne ein nachgeschaltetes Glühen bei einer Festigkeit von 400 N/mm² lediglich 7 % Bruchdehnung erreicht, da sich wegen der hohen Abkühlgeschwindigkeit ein höherer Perlitgehalt als im Sandguss einstellt. Dieser kann durch eine Wärmebehandlung weitgehend beseitigt werden, wodurch die Bruchdehnung dann steigt.
Umfassende Informationen über die Eigenschaften von GJS enthält die Quelle [46].
Eigenschaften bei erhöhten Temperaturen
Die Auswahl von Gusseisenwerkstoffen für den Einsatz bei erhöhten Temperaturen erfolgt im Wesentlichen unter den Gesichtspunkten der mechanischen Temperatur abhängigen Eigenschaften, der Beständigkeit gegen das Zundern, der Beständigkeit gegen das Wachsen und das Verändern des Gefüges und damit der Eigenschaften sowie der Temperaturwechselbeständigkeit.
Zundern
Das Zundern von unlegiertem Gusseisen mit Kugelgraphit beginnt bereits bei 250 °C, ist jedoch bis zu Temperaturen von etwa 400 °C so unbedeutend, dass es praktisch vernachlässigt werden kann. Nach zwanzig Jahren beträgt die Gewichtszunahme nur etwa 3 mg/cm2. Auch das geringe Zundern bei 450 °C stellt selten ein Problem dar. Ein Erhöhen der Temperatur auf 500 °C führt nach Bild 134 zu einem Verdoppeln der Verzunderungsrate, die aber noch immer relativ niedrig ist. Eine weitere Temperatursteigerung auf 550 °C verdoppelt erneut die Verzunderungsrate. Sie steigt bei noch höheren Temperaturen sehr rasch an. Das Zunderverhalten von Gusseisen mit Kugelgraphit in anderen oxidierenden Gasen ist dem hier beschriebenen Verhalten in Luft sehr ähnlich. Der Einfluss des Grundgefüges auf die Zunderbeständigkeit ist gering und vermindert sich mit steigender Temperatur. Das gilt auch mit Ausnahme des Siliciumgehaltes für die chemische Zusammensetzung.
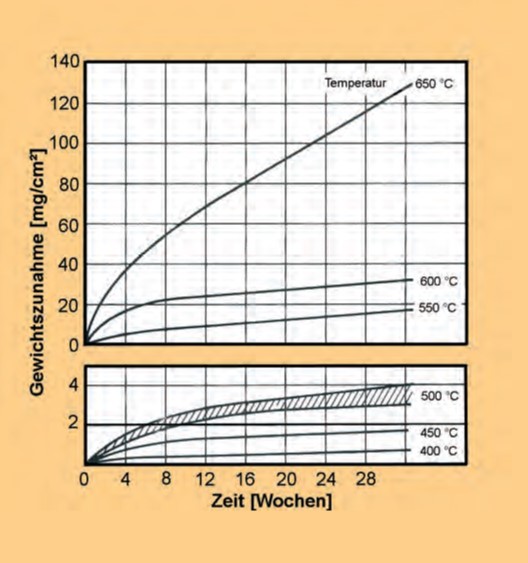
Durch Erhöhen des Siliciumgehaltes lässt sich die Zunderbeständigkeit deutlich steigern. Ab 4 % Silicium ist Gusseisen mit Kugelgraphit praktisch zunderbeständig. Mit 4 bis 5 % Silicium ähneln die mechanischen Eigenschaften von ferritischem GJS denjenigen von EN-GJS-600-3. Silicium legiertes zunderbeständiges Gusseisen mit Kugelgraphit ist stets ferritisch. Es kann bis zu der Temperatur eingesetzt werden, bei der die Ferrit-Austenit-Umwandlung beginnt. Wird diese Temperatur überschritten, so treten im Gefüge Volumenänderungen auf, die die schützende Zunderschicht aufreißen und Mikrorisse erzeugen, so dass der Oxidationsangriff erheblich beschleunigt wird. Gusseisen mit Kugelgraphit mit rund 4 % Si kann bis zu etwa 800 bis 820 °C eingesetzt werden, mit 5 % Si bis zu knapp 900 °C und mit 6 % Si bis 950 °C [116].
Wachsen
Die Volumenzunahme - das sogenannte Wachsen - von Gusseisenwerkstoffen bei längerem Halten oberhalb etwa 450 °C hat zwei Ursachen. Die eine ist der Zerfall des im Perlit oder als freier Zementit (Eisencarbid Fe3C) vorhandenen gebundenen Kohlenstoffs zu Graphit und Ferrit, die zweite ist die innere Oxidation, bei der Sauerstoff vor allem entlang des Graphits ins Werkstoffinnere vordringt, wobei die sich bildenden Oxide den Werkstoff aufblähen.
Gegen innere Oxidation ist Gusseisen mit Kugelgraphit weitgehend immun, da die Graphitkugeln nicht wie die Graphitlamellen beim Gusseisen mit Lamellengraphit zusammenhängen. Daher kann innere Oxidation nur an Oberflächenfehlern auftreten und äußert sich vorwiegend in Form von Blasen oder pickelartigen Aufwölbungen an der Oberfläche.
Die Volumenbeständigkeit von Gusseisen mit Kugelgraphit hängt vor allem von der Menge und der Stabilität des Perlits ab. So sind ferritische Sorten praktisch Wachstum beständig, rein perlitische können durch Zerfall des Perlits linear um 0,4 bis 0,5 % wachsen, was einer Volumenzunahme von 1,2 bis 1,5 % entspricht. Ist außerdem freier Zementit vorhanden, dann ist die Volumenzunahme entsprechend größer. Warmfeste, mit Molybdän legierte Sorten enthalten häufig einen geringen Anteil gebundenen Kohlenstoffs in Form von molybdänreichen Carbiden. Diese sind im Gegensatz zu Eisencarbid (Fe3C, Zementit) chermisch stabil, so dass ein derartiges Gusseisen mit Kugelgraphit Wachstum beständig ist, sofern die übrige Grundmasse völlig ferritisch ist.
Der Perlitzerfall und damit das Wachsen von unlegiertem Gusseisen mit Kugelgraphit beginnt bereits bei etwa 450 °C und nimmt mit steigender Temperatur rasch zu [113]. Er lässt sich durch das zum Einstellen eines perlitischen Gefüges bei ENGJS- 600-3 oder EN-GJS-700-2 verwendete Legierungselement Kupfer nicht verlangsamen. Dies ist nur möglich durch niedrige Silicium- und Kohlenstoffgehalte, die Verwendung eines an Spurenelementen reichen Einsatzmaterials, den Zusatz von 0,1 % Zinn oder das allerdings in der Regel kaum zulässige Legieren mit 0,3 % Chrom. Bei höherer Temperatur reichen allerdings auch diese Maßnahmen nicht mehr aus.
Wird für längere Zeit Volumenbeständigkeit gefordert, kann für Einsatztemperaturen oberhalb 400 bis 450 °C nur ferritisches Gusseisen mit Kugelgraphit eingesetzt werden. Bei durch Temperaturwechsel beanspruchten Bauteilen kann es zu Maßänderungen kommen, deren Ursache nicht innere Oxidation oder Gefügeänderungen sind, sondern alternierende, über der Warmfließgrenze liegende Zug- und Druckspannungen.
Warmfestigkeit
Im Gegensatz zu Gusseisen mit Lamellengraphit, dessen Festigkeit sich bis zu etwa 300°C kaum ändert, führt eine Temperaturerhöhung bei Gusseisen mit Kugelgraphit sofort zu einem Abfall der Festigkeit. Dies gilt vor allem für die perlitischen Sorten, wie aus Bild 135 hervorgeht. Warmzugfestigkeit und Warmdehngrenze sind innerhalb der Streubänder abhängig von der chemischen Zusammensetzung. Sie nehmen mit höheren Mangan-, Phosphor- und Siliciumgehalten sowie durch Zusatz von Molybdän oder Nickel zu. Die Wirkung von Silicium wird im Bild 135 durch die eingetragenen Werte für hitzebeständiges ferritisches Gusseisen mit 4 % Silicium verdeutlicht. Aus dem Bild ist zudem ersichtlich, dass die Bruchdehnung ein Minimum zwischen 200 und 400 °C hat. Die Härte fällt bis etwa 350 °C allmählich und darüber steil ab.
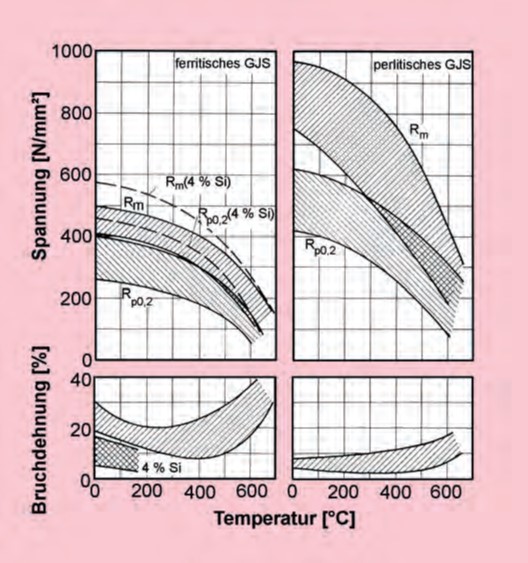
Die Kerbschlagarbeit von ferritischem Gusseisen mit Kugelgraphit nimmt mit steigender Temperatur langsam ab, sinkt aber bis 600 °C nicht unter den Wert der Tieflage. Bei perlitischem Gefüge erfolgt zunächst eine Zunahme bis in die Hochlage, die unter Umständen erst bei 200 bis 300 °C erreicht wird, und dann erst eine Abnahme.
Der Elastizitätsmodul von Gusseisen mit Kugelgraphit wird mit steigenden Temperaturen zunächst wenig und dann stärker vermindert. Bei perlitischen Sorten nimmt er von ~ 175 bei RT auf ~150 kN/mm2 bei 550 °C ab, bei ferritischen Sorten von ~160 bei RT auf ~135 kN/mm2 bei 450 °C [118]. Es ist zu berücksichtigen, dass der im Zugversuch bestimmte und üblicherweise als E-Modul angegebene statische Wert niedriger ist als der mit Schwingungsmessungen bestimmte dynamische EModul. Weiterhin ist zu beachten, dass eine Spannungs- beziehungsweise Dehnungsabhängigkeit beider E-Module besteht, die ebenfalls einem Temperatureinfluss unterliegen [119].
Zeitstandeigenschaften
Für die Bemessung von Druckbehältern und Armaturen aus Gusseisen mit Kugelgraphit gilt das AD-2000 Merkblatt W 3/2 mit den in Tabelle 10 genannten Werten für die 0,2-%-Dehngrenze und Betriebstemperaturen bis 350 °C.
Tabelle 10: 0,2-%-Dehngrenze von GJS für die Berechnung von Druckbehältern und Sicherheitsbeiwerte (nach AD-2000-Merkblatt W3/2 von 2003)
| Werkstoff EN-... | 0,2-%-Dehngrenze [N/mm2] | Sicherheits- beiwert S | |||||||
| Wanddicke: bis 60 mm | Wanddicke: 60 bis 200 mm | ||||||||
| Betriebstemperatur in °C bis | |||||||||
| 20 (50) | 150 | 250 | 350 | 20 (50) | 150 | 250 | 350 | ||
| GJS-350-22RT | 220 | 200 | 170 | 140 | - | - | - | - | 2,4 |
| GJS-400-18RT | 250 | 230 | 200 | 160 | 230 | 210 | 180 | 150 | 2,4 |
| GJS-400-15 | 250 | 230 | 200 | 160 | 230 | 210 | 180 | 150 | 3,5 |
| GJS-500-7 | 320 | 290 | 250 | 200 | 260 | 240 | 200 | 160 | 4,0 |
| GJS-600-3 | 380 | 350 | 310 | 230 | 320 | 290 | 260 | 190 | 5,0 |
| GJS-700-2 | 440 | 410 | 370 | 300 | 360 | 330 | 300 | 250 | 5,0 |
Die Streubänder der 1000-h-Zeitstandfestigkeit von unlegiertem Gusseisen mit Kugelgraphit sind in Abhängigkeit von der Temperatur im Bild 137a dargestellt. Die anfänglich höhere Festigkeit der perlitischen Sorten nimmt mit steigender Temperatur ab und nähert sich der der ferritischen Sorten. Bei längeren Beanspruchungszeiten über 450 °C ist zudem mit zumindest teilweisem Zerfall des Perlits zu rechnen, wodurch die Festigkeit verringert wird. Angaben über das Kriechverhalten von unlegiertem Gusseisen mit Kugelgraphit im Temperaturbereich um 400 °C enthält Bild 137b. Wie aus den Bilder 137c und 137d ersichtlich, lassen
sich die Zeitstandeigenschaften durch Zusatz von Legierungselementen verbessern. In erster Linie wird Molybdän, seltener Nickel verwendet.
Bei Druckbeanspruchung ist die Abhängigkeit des Kriechverhaltens von der Temperatur ähnlich wie bei Zugbeanspruchung, was im Bild 137e für ferritisches und perlitisches Grundgefüge bei 400 und 450 °C gezeigt wird. Für längere Beanspruchungszeiten können, um jede Maß- und Eigenschaftsänderung durch Perlitzerfall auszuschließen, nur ferritische Sorten verwendet werden.
Dem starken Oxidationsangriff bei Einsatztemperaturen über 600 °C wird mit einem Siliciumgehalt von über 4 % begegnet. Ein Legieren mit Molybdän verbessert außerdem die Zeitstandeigenschaften. Werte für die Zeitstandfestigkeit und die Kriechgeschwindigkeit solcher Werkstoffe, die häufig mit dem Kurznamen GJS-SiMo bezeichnet werden, sind für 705 °C in den Bildern 137f und 137g enthalten (siehe aus Kapitel 10. 4). Die höchstmögliche Einsatztemperatur für ein Gusseisen mit etwa 4 % Silicium ist 820 °C. Bei höherer Temperatur beginnt die Ferrit-Austenit-Umwandlung, die den Werkstoff recht rasch zum Erliegen bringt.
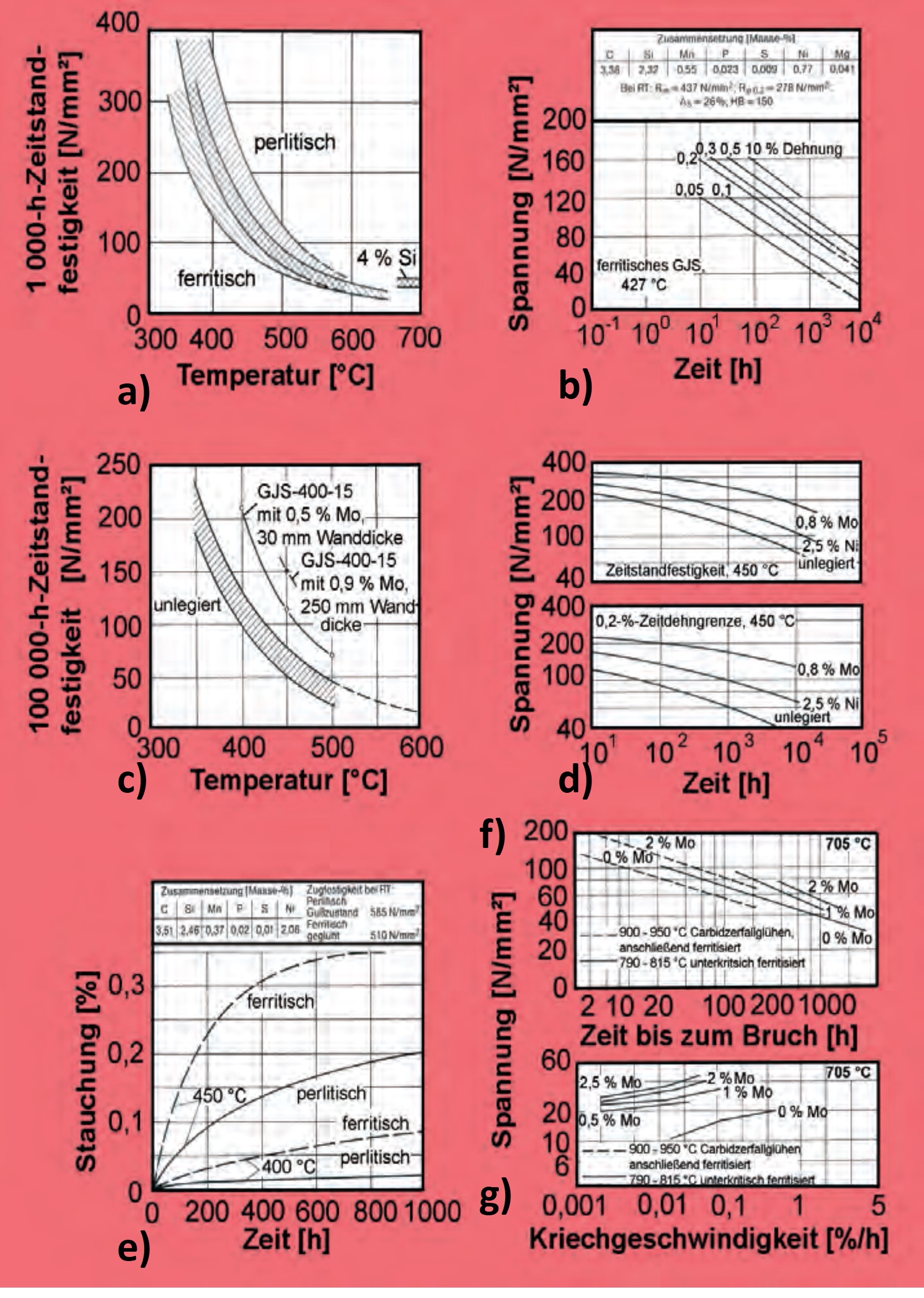
a) Temperaturabhängigkeit der 1000-h-Zeitstandfestigkeit von GJS (nach [118, 120])
b) Kriechverhalten von ferritischem GJS bei 427 °C (nach [120])
c) Einfluss von Temperatur, Wanddicke und Molybdängehalt auf die 100 000-h-Zeitstandfestigkeit von GJS (nach [121])
d) Zeitstandfestigkeit und Zeitdehngrenze von unlegiertem und legiertem ferritischen GJS mit 3,6 % C; 2,4 % Si; 0,3 % Mn; 0,05 % P, 0,006 % S; und 0,045 % Mg (nach [122])
e) Kriechverhalten eines perlitischen und eines ferritischen GJS bei 400 und 450 °C unter 230 N/mm² Druckspannung (nach [123])
f) Typische Werte für die Zeitstandfestigkeit von GJS mit 4 % Si bei 705 °C in Abhängigkeit vom Molybdängehalt und Ferritisierungsverfahren (nach [116])
g) Typische Werte für die Kriechgeschwindigkeit von GJS mit 4 % Si bei 705 °C in Abhängigkeit vom Molybdängehalt und Ferritisierungsverfahren (nach [116])
Ein Verspröden von Gusseisen mit Kugelgraphit, wie beispielsweise die 475-°CVersprödung bei manchen Stählen, tritt auch nach langzeitigem Halten bei 400 bis 500 °C nicht auf.
Temperaturwechselbeständigkeit
Häufige Temperaturwechsel stellen eine starke Beanspruchung der Bauteile dar und können diese durch Risse oder Verformungen unbrauchbar machen. Ursache sind Spannungen, die aufgrund eines behinderten thermischen Ausdehnens oder Zusammenziehens entstehen. Sie sind der Temperaturdifferenz, dem Elastizitätsmodul und dem thermischen Ausdehnungskoeffizienten des Werkstoffs proportional. Die entstehenden Zugspannungen können in manchen Fällen fast Werte wie bei der Zugfestigkeit erreichen oder diese sogar überschreiten, so dass sehr schnell Risse auftreten. Gewöhnlich bilden sich diese nach einer bestimmten Zahl von Temperaturwechseln infolge Überschreitens der Dauerwechselfestigkeit.
Gusseisen mit Kugelgraphit besitzt aufgrund seiner hohen Zugfestigkeit, Dauerwechselfestigkeit und Bruchdehnung bei Raumtemperatur eine gute Beständigkeit gegen Rissbildung. Andererseits sind aber die entstehenden Spannungen wegen des höheren Elastizitätsmoduls deutlich größer als die von Gusseisen mit Lamellengraphit.
Das Verhalten von Gusseisen mit Kugelgraphit hängt von der Art der Temperaturwechselbeanspruchung ab. Bei sehr schroffen Temperaturänderungen, die allerdings in der Praxis kaum auftreten, kann es aufgrund der niedrigeren Wärmeleitfähigkeit eher zu Brandrissen kommen als bei Gusseisen mit Lamellengraphit. Bei langsamer Abkühlgeschwindigkeit wirken sich dagegen die höhere Festigkeit und Duktilität des Gusseisens mit Kugelgraphit aus, so dass die Brandrissbeständigkeit in der Regel höher ist als die von Gusseisen mit Lamellengraphit [115, 118, 124].
Gusseisen mit Kugelgraphit hat eine starke Neigung zum Verzug. Dies ist eine Folge des hohen Elastizitätsmoduls, der bei Temperaturdifferenzen zu großen Spannungen führt. Diese können vor allem bei unlegierten, ferritischen Sorten die relativ niedrige Dehngrenze überschreiten und damit zu Verzug und Verformung des Bauteils führen.
Aufgrund seiner hohen Festigkeit hat perlitisches Gusseisen mit Kugelgraphit die höchste Beständigkeit gegen Rissbildung und Verzug, sofern der Perlit nicht als Folge der Temperaturbelastung zerfällt.
Der Perlitzerfall wird durch Temperaturwechselbeanspruchung und Spannungen zudem deutlich beschleunigt.
Die Temperaturwechselbeständigkeit von ferritischem Gusseisen mit Kugelgraphit kann durch Erhöhen der Warmfestigkeit, also durch Legieren mit Molybdän, deutlich verbessert werden. Es hat sogar eine höhere Temperaturwechselbeständigkeit als unlegierte perlitische Sorten, obwohl diese bei Raumtemperaturen höhere Festigkeit haben.
Physikalische Eigenschaften
Die für Gusseisen mit Kugelgraphit zum Einsatz bei erhöhten Temperaturen wichtigsten physikalischen Eigenschaften sind die Wärmeleitfähigkeit beziehungsweise Temperaturleitfähigkeit und der thermische Ausdehnungskoeffizient.
Die Wärmeleitfähigkeit hängt in erster Linie von der Grundmasse, dem Siliciumgehalt und anderen in der Grundmasse gelösten Elementen, z.B. Nickel, und dem Graphitgehalt ab. Mit steigendem Graphitgehalt nimmt die Wärmeleitfähigkeit zu, jedoch in geringerem Maße als bei Gusseisen mit Lamellengraphit. Erhöhen des Siliciumgehaltes und auch des Nickelgehaltes senken die Wärmeleitfähigkeit. Tabelle 11 enthält Mittelwerte für die Wärmeleitfähigkeit. Bei ferritischem Gusseisen mit Kugelgraphit senkt ein von 2 auf 3 % erhöhter Siliciumgehalt die Wärmeleitfähigkeit von 39 auf rund 37,5 W/(m . K).
Tabelle 11: Anhaltswerte für die Wärmeleitfähigkeit von GJS bei Temperaturen bis 500 °C (nach [116, 121])
| Werkstoff EN-... | Wärmeleitfähigkeit [W/(m.K)] bei | ||||
| 100°C | 200°C | 300°C | 400°C | 500°C | |
| GJS-350-22RT | 40,2 | 43,3 | 41,5 | 38,8 | 36,0 |
| GJS-400-15 | 38,5 | 41,5 | 39,8 | 37,4 | 35,0 |
| GJS-500-7 | 36,0 | 38,8 | 37,4 | 35,3 | 33,5 |
| GJS-600-3 | 32,9 | 35,4 | 34,2 | 32,8 | 31,6 |
| GJS-700-2 | 29,8 | 32,0 | 31,0 | 30,3 | 29,8 |
| 4SiMo | 25,1 | 27,2 | 28,1 | 28,6 | 28,9 |
Der thermische Ausdehnungskoeffizient von Gusseisen mit Kugelgraphit hängt nur wenig vom Grundgefüge und der chemischen Zusammensetzung ab, sofern es sich nicht um autenitisch-feriitisches oder austenitisches Gefüge handelt. In der Tabelle 12 sind mittlere Werte in Abhängigkeit von der Temperatur angegeben. Perlitisches Gefüge hat aufgrund des geringeren thermischen Ausdehnungskoeffizienten des Zementits etwas niedrigere Werte als ferritisches Gefüge. Mit steigender Temperatur nimmt der thermische Ausdehnungskoeffizient zu.
Physikalische Eigenschaften
Tabelle 12: Mittlerer thermischer Ausdehnungskoeffizient von ferritischem und perlitischem GJS im Temperaturbereich von 20 bis 500 °C [nach [116, 121])
| Werkstoff EN-... | Wärmeleitfähigkeit [W/(m.K)] bei | ||||
| 100°C | 200°C | 300°C | 400°C | 500°C | |
| GJS-400-15 (ferritisch) | 11,2 | 11,9 | 12,5 | 13,0 | 13,4 |
| GJS-700-2 (perlitisch) | 11,1 | 11,7 | 12,3 | 12,8 | 13,2 |
| 4SiMo (ferritisch) | 10,7 | 12,7 | 13,4 | ||
Sprunghaft ändert sich der thermische Ausdehnungskoeffizient, wenn es zu einer Gefügeumwandlung kommt, sei es zum Zerfall von Perlit zu Ferrit und Graphit, was eine erhebliche Ausdehnung verursacht, sei es, dass die Ferrit-Austenit-Umwandlung durchlaufen wird, da es hier ebenfalls zu einem Volumensprung kommt und zudem Austenit einen größeren Ausdehnungskoeffizienten als Ferrit hat.
Eigenschaften bei niedrigen Temperaturen
Die steigende Verwendung von Gusseisen mit Kugelgraphit im Fahrzeugbau, bei Windenergieanlagen und für Armaturen führt in zunehmendem Maße zum Einsatz bei niedrigen Temperaturen. Dabei findet der Bereich der arktischen Temperaturen (um -40 bis -60 °C) besonderes lnteresse. Dieser Temperaturbereich lässt sich natürlich mit austenitischen Werkstoffen sehr gut beherrschen. Im Zeichen steigender Energie- und Rohstoffkosten drängt sich zwangsläufig die Frage auf, ob es für diesen an übliche Einsatztemperaturen grenzenden Bereich nicht möglich ist, auch unlegierte Werkstoffe zu verwenden, zumal bis zu -40 °C für EN-JS-
350-22-LT und - 20 °C für EN-GJS-400-18-LT nach DIN EN1564 ohnehin Garantien (über das Kerbschlagverhalten) abgegeben werden müssen.
Kerbschlagverhalten
Das Kerbschlagverhalten ist jedoch nicht allein entscheidend. Einmal lässt sich Schlagzähigkeit durch Wanddicke ersetzen [125], zum zweiten erfolgt die Grundbelastung meist nicht schlagartig, und schließlich vermeidet man im allgemeinen bei jeder Konstruktion scharfe äußere Kerben. Damit aber wird die Übergangstemperatur zwischen duktilem und sprödem Verhalten zum Teil deutlich zu niedrigeren Temperaturen verschoben.
Weiterhin ist die Schlagzähigkeit beziehungsweise die Schlagarbeit ohnehin keine Kennzahl, mit der konstruiert werden kann, sondern letztlich ein Anhalt dafür, dass beim Überschreiten der Belastbarkeit Energie durch plastische Formänderung unschädlich gemacht und nicht in kinetische Energie (= umherfliegende Bruchstücke) verwandelt wird. Gerechnet werden kann und muss vielmehr mit Festigkeitskennwerten und insbesondere - häufig stellvertretend für andere - mit Streckgrenze oder Dehngrenze. Im Übrigen ist die Schlagzähigkeit bei weitem nicht der einzige Maßstab für die Duktilität eines Werkstoffes. Bei geringer Belastungsgeschwindigkeit sind vielmehr Bruchdehnung und Brucheinschnürung genauso interessant und für das Werkstoffverhalten sogar aussagefähiger. So ist es denn auch unter Berücksichtigung der Erkenntnisse der Bruchmechanik nach wie vor interessant zu wissen, wie die Ergebnisse von Zugversuchen bei niedrigen Temperaturen aussehen.
Am besten wäre es natürlich, wenn für gemäßigte Zonen geeignete Geräte und Werkzeuge ohne Änderung auch in klimatisch ungünstigen Gebieten einsetzbar wären. Das ist zweifellos um so eher möglich, je spröder sich der Werkstoff bei Raumtemperatur verhält. Denn wenn ein Werkstoff bei Raumtemperatur vollständig spröde ist, wird seine Schlagempfindlichkeit auch bei -50 °C nicht größer werden.
Festigkeitseigenschaften
Nach [126, 127] nimmt die Elastizitätsgrenze Rp bei allen Sorten mit sinkender Temperatur linear und mit gleichem Steigungsmaß zu. Die Kurven für die 0,2-%-Dehngrenze von EN-GLS-400-15 und ENGJS-500-7 steigen mit sinkender Temperatur überproportional und parallel zueinander an, die von EN-GJS-600-3 und GJS-700-2 mit bei Raumtemperatur gleicherAusgangssteigung linear und ebenfalls parallel.
Wie aus Bild 139a zu entnehmen, wird offensichtlich die Temperaturabhängigkeit der Zugfestigkeit durch den Perlitgehalt „gedreht“, und zwar um einen Punkt, der bei etwa -125 °C und etwa 500 N/mm2 liegt. Mit steigendem Perlit (also geringer werdendem Ferrit-)Gehalt geht mit sinkender Temperatur der Anstieg der Kurven in einen Abfall über. Der Perlitgehalt, bei dem die Festigkeit von der Temperatur in dem hier untersuchten Bereich völlig unabhängig ist, dürfte bei über 50 % liegen, wenn davon ausgegangen wird, dass EN-GJS-500-15 mit noch relativ hoher Dehnung üblicherweise auch einen recht hohen Ferritgehalt hat.
Der Elastizitätsmodul zeigt einen ähnlichen Verlauf wie die Elastizitäts- und 0,2-%-Dehngrenze, wie am Beispiel von ENGJS-500-15 im Bild 139b zu erkennen ist. Er nimmt mit sinkender Temperatur leicht zu. Interessant ist, dass bei hohen Temperaturen stärkere Abweichungen nach unten, bei niedrigeren Temperaturen stärkere Abweichungen nach oben auftreten. Dem Verlauf der Hüllkurve zufolge ist also eine steilere Temperaturabhängigkeit zu erwarten.
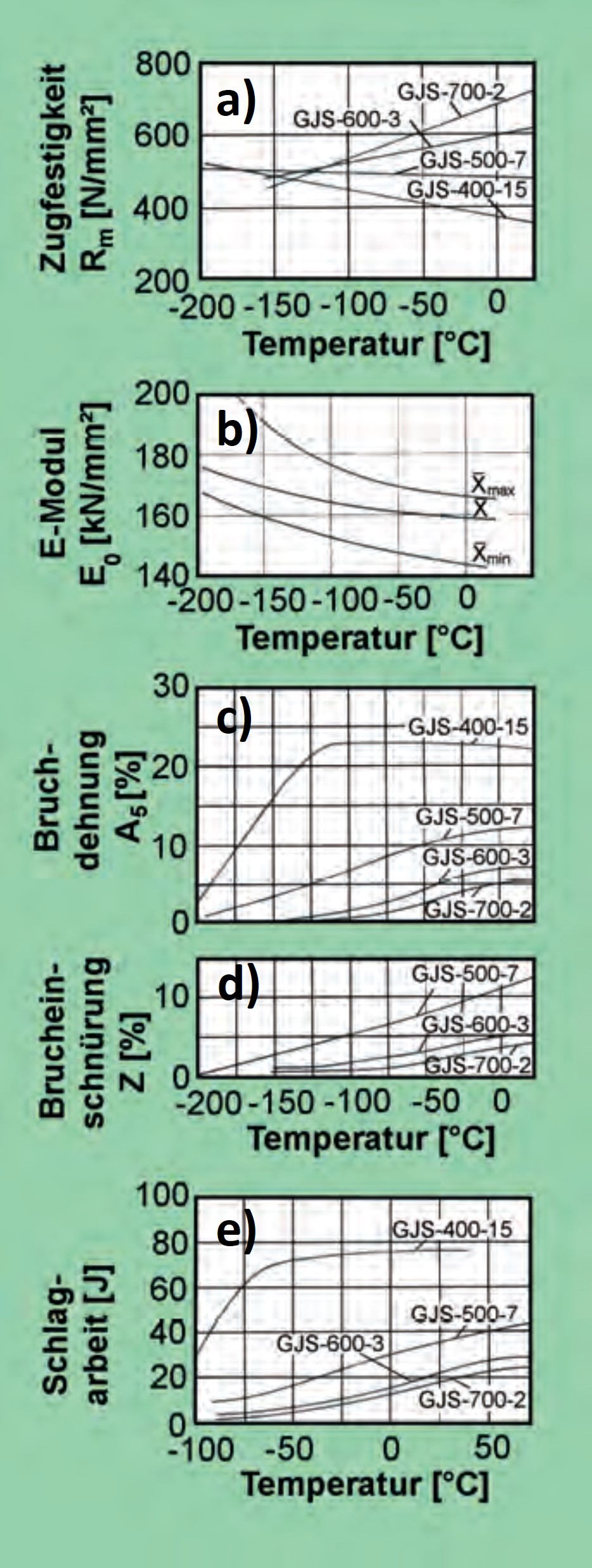
a) extrapolierter Festigkeitsverlauf von GJS bei abnehmenden Temperaturen
b) E-Modul von EN-GJS-500-7 bei abnehmender Temperatur
c) Hochlage und Übergangstemperatur von Bruchdehnung und Brucheinschnürung für einige GJS-Sorten
d) Verlauf der Schlagarbeit in Abhängigkeit von der Temperatur bei einigen GJS-Legierungen
Nach Untersuchungen an ferritischem Gusseisen mit Kugelgraphit [128, 129] zeigt sich ein überproportionaler Anstieg der 0,2-%-Dehn- und Stauchgrenzen mit sinkender Temperatur, wobei das Verhältnis Stauch- zu Dehngrenze über den gesamten Temperaturbereich mit etwa 1,05 konstant bleibt. Auch die Zugfestigkeit steigt nach diesen Untersuchungen unterhalb Raumtemperatur überproportional an, wobei das Dehngrenzenverhältnis sich mit sinkender Temperatur dem Wert 1 nähert. Da bei duktilen Werkstoffen eine Druckfestigkeit nicht zu bestimmen ist, wurde die 8-%-Stauchgrenze ermittelt, die ebenfalls mit sinkender Temperatur ansteigt, aber auch bei -196 °C noch deutlich über der 0,2-%-Stauchgrenze bleibt.
Die Temperaturabhängigkeit der mechanischen Eigenschaften von austenitischferritischem Gusseisen mit Kugelgraphit lässt sich ohne weiteres in den gezeigten Rahmen der ferritischen bis perlitischen Sorten einordnen [130].
Zähigkeitseigenschaften
Bruchdehnung und Brucheinschnürung (Bild 139c) sowie an verformten Proben gemessene Schlagarbeit (Bild 139d) verhalten sich sehr ähnlich. Von EN-GJS-400-15 zu EN-GJS-500-7 nimmt die Hochlage von Bruch-dehnung und Schlagarbeit stark ab, von EN-GJS-500-7 zu EN-GJS-600-3 weniger stark und von EN-GJS-600-3 zu EN-GJS-700-2 kaum noch. Die Übergangstemperaturen steigen mit zunehmender Festigkeit. Bei der GJS-400-15-Kurve ist der Abfall im Bereich der Übergangstemperatur etwas steiler. Allerdings ist bei der Bruchdehnung der Abstand von Hoch- und reiner Tieflage mit etwa 75 K immer noch recht groß.
Spezielle Anforderungen an Windenergieanlagengussteile
Erst in den 1990er Jahren, 20 Jahre nach der ersten Ölkrise wurde die Windkraft als ernst zu nehmende Alternative für die Energieversorgung definiert und bis 2002 wurden in Europa für 32 000 MW Windkraftwerke installiert. Die damals für 2007 prognostizierte Zahl einer jährlichen Steigerung um rd. 15 bis 17 % bis auf 58 000 bis 60 000 MW in Europa allein bewahrheitet sich. Nach oben tendiert auch die Größe der einzelnen Anlagen. Die Zwerge von 1980 mit 0,03 MW, einer Höhe von 30 m und einem Rotordurchmesser von 15 m sind bis auf 5 MW und 130 beziehungsweise 115 m angewachsen (Bild 140).

Wichtige Bauteile im Gondel- und Getriebebereich sind Gussteile aus Gusseisen mit Kugelgraphit (Bild 141).

1 - Maschinenträger;
2 - Stratorstern,
3 - Achszapfen,
4 - Rotornabe,
5 - Blattadapter
Die andalusische Westküste dürfte an die Gussstücke ihrer Aberhunderte von Windkraftwerken, die mehr durch ihre Konzentration als ihre Größe beeindrucken, weniger abverlangen als das raue Klima an und in der Nordsee oder in arktischen Gebieten. So bestehen in dortigen Anlagen die Gussteile grundsätzlich aus dem für tiefe Temperaturen geeignetem Werkstoff EN-GJS-400-18-LT, ob es sich dabei um das Abstützrohr für die Gondel, eine Rotornabe mit Adapter zum Rotorblatt oder ein anderes Gussteil handelt. Die herausragende Eigenschaft dieses Werkstoffs ist die ISO-V-Kerbschlagarbeit bei -20 °C, die mit >12 J zu gewährleisten ist (Tabelle 13). Die chemische Zusammensetzung mit 3,3 bis 3,5 % C, 1,9 bis 2,2 % Si, < 0,15 % Mn, < 0,030 % P, 0,008 bis 0,012 % S und 0,04 % Mg (Empfehlung) spiegelt diese Forderung sowohl qualitativ als auch quantitativ deutlich wieder.
Tabelle 13: Mechanische Eigenschaften (gewährleistete Mindest- und Anhaltswerte) von EN-GJS-400-18LT (nach [131])
| Eigenschaft | Maßgebende Wanddicke T [mm] | Gemessen an | |
| getrennt gegossenen Probestücken | angegossenen Probestücken | ||
| Zugfestigkeit Rm [N/mm2] | < 30 30 bis 60 60 bis 200 | > 400 | > 400 > 390 > 370 |
| 0,2%-Dehngrenze Rp0,2 [N/mm2] | < 30 30 bis 60 60 bis 200 | > 240 | > 240 > 230 > 220 |
| Bruchdehnung A [%] | < 30 30 bis 60 60 bis 200 | > 18 | > 18 > 15 > 12 |
| ISO-V-Kerbschlagarbeit AISO-V Mittelwert bei -20 °C [J] | 30 bis 60 60 bis 200 | > 12 | > 12 10 |
| Härte HB 30 | 120 bis 160 | ||
| Elastizitätsmodul E [kN/mm2] | 160 bis 180 | ||
| Schubmodul [kN/mm2] | ~ 0,4 · E | ||
| Druckfestigkeit σdB [N/mm2] | 700 | ||
| Biegewechselfestigkeit σbW [N/mm2] | +/- 200 | ||
| Zug-Druck-Wechselfestigkeit σzdW [N/mm2] | +/- 110 | ||
| Bruchzähigkeit KIC[N/mm²¬m] | 30 | ||
Weitere Carbid stabilisierende Elemente oder solche, die um die Graphiteinschlüsse Diffusionsbarrieren bilden können, müssen auf Spurenniveau gehalten werden. Alles, was versprödet, wie etwa das Phosphideutektikum, wird restriktiv behandelt (Bild 143a). Selbst Silicium ist davon betroffen (Bild 143b), das im Hinblick auf das gewünschte hohe Graphitisierungspotential zwar so hoch wie nötig, wegen der Versprödung des Ferrits aber so niedrig wie möglich einzustellen ist.
Das Gefüge der Gusssteile muss folgende Merkmale aufweisen:
- Anzahl Graphitkugeln von 100 bis 200 Kugeln/mm² (Höhere Kugelzahlen gefährden den AISO-V-Wert, niedrigere steigern die Gefahr des Ausscheidens spröder interzellularer Phasen!);
- eine Nodularität von min. 95 %;
- eine regelmäßige Kugelform (Unregelmäßig ausgebildete Graphitkugeln können Riss auslösend wirken!);
- eine vollferritische Matrix; (Perlit oder andere an den Zellen- oder Kolonienrändern geseigerte Carbide oder nichtmetallische Einschlüsse sind nicht zulässig!) (Bild 143c)
- keinerlei Mikroporen und/oder Dross im Gussteil.
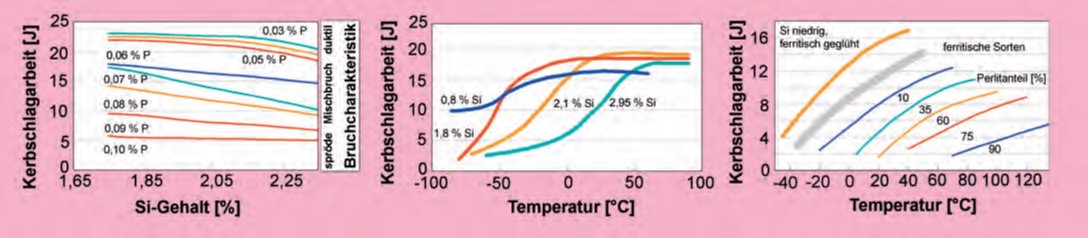
a) Mit steigenden Gehalten an Phosphor und Silicium sinkt die Kerbschlagarbeit bei ferritischem GJS (nach [132])
b) Mit sinkendem Siliciumgehalt sinkt die Übergangstemperatur von zähem zu sprödem Bruch (nach [133])
c) Nur ein voll ferritisches Gefüge eines niedrig silicierten GJS kann den Ansprüchen auf hohe Kerbschlagarbeit bei niedrigen Temperaturen gerecht werden (nach [133])
Aus diesen Forderungen ergeben sich die bei der Gussherstellung einzustellenden Parameter ganz von allein:
- Reine Einsatzstoffe (etwa 40 % Spezialroheisen, arteigenes Kreislaufmaterial, hochreiner Stahlschrott);
- Behandlung mit Magnesium unter Vermeidung von Mg-Restgehalten über 0,045 % und Verwendung von Vorlegierungen mit möglichst niedrigen Gehalten an Magnesium und Silicium;
- Kontrollierte, gegebenenfalls in zwei Stufen durchzuführende Impfung; (Die in der chemischen Zusammensetzung vorgesehene untere Grenze für den Schwefelgehalt berücksichtigt die Anwendung von Impfmitteln, die unter Bildung von Sulfiden keimwirksam werden. Die Keimbildung sollte in mehreren aufeinander folgenden Wellen erfolgen.);
- Die Gießtemperatur, üblicherweise zwischen 1370 und 1400 °C angesiedelt, ist stückabhängig unter Berücksichtigung der verwendeten Speisetechnik zu bestimmen (So weit wie möglich soll das Eisen unter Nutzung des eigenen Speisungsvermögens erstarren. Die Expansion des eutektischern Graphits soll zu diesem Zweck in mehreren Erstarrungswellen geschehen. Ergebnis eines solchen Erstarrungsablaufs ist unter anderem eine aus mindesten zwei voneinander signifikat verschiedenen Kollektiven bestehende Größen-Mischverteilung der Graphitkugeln [134]);
- Die Formen und Kerne müssen fest, das heißt gut verdichtet sein, damit sie dem Kristallisationsdruck des Graphits widerstehen und dadurch die Eigenspeisung unterstützen können (Im
übrigen gilt für die gewünschte schnelle Formfüllung die Regel: Lieber eine Luftpfeife zu viel als eine zu wenig setzen!).
Trotz all dieser Forderungen und restriktiver Randbedingungen ist heute gängige Praxis, Gussteile sämtlicher Größenordnungen aus EN-GJS-400-18-LT im Gusszustand, das heißt ohne kostspielige ferritisierende Wärmebehandlung herzustellen.
Verschleißverhalten
Unter Verschleiß versteht man einen auf mechanischen Ursachen beruhenden fortschreitenden Materialverlust auf der Oberfläche eines festen Körpers. Eine Verschleißbeständigkeit als Werkstoffkenngröße gibt es nicht, sondern das Verschleißverhalten hängt vom Tribosystem (Grundkörper, Gegenkörper oder - stoff und Randbedingungen wie Umgebungsmedium, Bewegungsrichtung oder Anpressdruck) ab. Die für Gusseisen mit Kugelgraphit wichtigsten Verschleißmechanismen sind Abrasion, die mit mineralischen Gegenkörpern vor allem im Bereich der Steine- und Erden-lndustrien auftritt, und Adhäsion und Oberflächenzerrüttung mit metallischen Gegenstoffen.
Abrasivverschleiß
Die Abrasiv-Beständigkeit von Eisenwerkstoffen hängt vom in der Grundmasse gelösten oder als Carbid ausgeschiedenen Kohlenstoffgehalt und der Ausbildung der Grundmasse ab [135, 136]. Die Härte im Anlieferungszustand ist kein zuverlässiges Maß für die Verschleißbeständigkeit, aber als Indikator für das Grundgefüge eines bestimmten Werkstoffes brauchbar.
Im Bild 144 [137] sind beispielhaft die Streufelder der im Schleißtopfversuch bestimmten Verschleißbeständigkeiten verschiedener Eisenwerkstoffe über der Härte dargestellt. Gusseisen mit Kugelgraphit EN-GJS-600-3 bis EN-GJS-800-2 liegen in der Mitte des Streufeldes unlegierter und niedrig legierter Stähle gleicher Härte. EN-GJS-700-2 verhält sich etwa wie ein normalisierter unlegierter Stahl mit 0,5 % C. EN-GJS-500-7 und EN-GJS-400-15 sind aufgrund ihres an Kohlenstoff ärmeren weitgehend ferritischen Grundgefüges weniger verschleißbeständig, so dass zum Beispiel EN-GJS-400-15 zwischen GE240 und GE260 liegt.
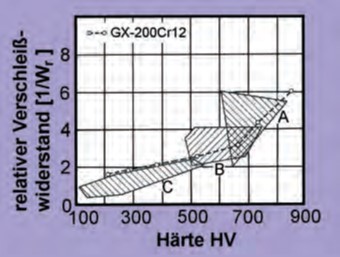
A - martensitisches weißes Gusseisen, Ni-Cr-legiert
B - perlitisches weißes Gusseisen, un- und niedrig legiert
C - Stähle mit 0,15 bis 0,5 % C, graues Gusseisen mit Kugelgraphit
Die völlig oder überwiegend ferritischen Sorten sind daher für Bauteile, die abrasivem Verschleiß unterliegen, nicht gut geeignet. Werden diese Werkstoffe aus anderen Gründen, zum Beispiel wegen ihrer höheren Zähigkeit oder besseren Bearbeitbarkeit, eingesetzt, können sie mit einer verschleißbeständigen Beschichtung versehen werden. So hat sich zum Beispiel bei REA-Pumpen eine Beschichtung aus polymergebundenen SiC gut bewährt [1438. Die perlitischen Sorten sind verschleißbeständiger und zwar umso mehr, je dichter und feinstreifiger der Perlit ist, so dass in der Regel die Verschleißbeständigkeit von EN-GJS-700-2 bis EN-GJS-900-2 beziehungsweise ENGJS-HB265 bis EN-GJS-HB330 zunimmt.
Austenitisch-ferritische, bainitisch-austenitische oder martensitische Gusseisen mit Kugelgraphit (siehe Kapitel 10) haben einen Verschleißwiderstand, der vielen niedriglegierten Vergütungsstählen wie zum Beispiel 42CrMo4 [139] überlegen ist, und können sogar die Werte von Manganhartstahl oder verschleißbeständigem martensitischem Gusseisen EN-GJN-HV520 (Ni-Hard 2) nach DIN EN 12513 erreichen oder sogar übertreffen [136]. Insbesondere austenitisch-ferritisches Gusseisen mit Kugelgraphit (ADI) nach DIN EN 1564 zeichnet sich durch eine günstige Kombination von Verschleißbeständigkeit und Zähigkeit aus. Das Grundgefüge dieser Sorten wird in der Regel durch eine Wärmebehandlung erzeugt, kann aber, wenn die Vergütung wegen der Größe und Form der Gussstücke zu schwierig erscheint, auch im Gusszustand (zum Beispiel GX300NiMo3Mg nach DIN 1695) erreicht werden.
Besonders hohe Verschleißbeständigkeit haben Verbundgussstücke aus perlitischem oder austenitisch-ferritischem Gusseisen mit Kugelgraphit mit einer Randschicht aus eingegossenem Hartmetall in Form von Granulat oder Platten.
Metall-Metall-Verschleiß
Die Verschleißmechanismen bei metallischen Werkstoffpaarungen sind Adhäsion (örtliches Verschweißen und im Extremfall Fressen) bei Gleitbewegung, Oberflächenzerrüttung bei Roll- und Wälzbewegung und bei Anwesenheit von Verschleißstaub oder Verschmutzung auch Abrasion. Durch Schmieren und geeignete Werkstoffpaarung soll vor allem die Adhäsion ausgeschaltet oder wenigstens gering gehalten werden.
Oft ist der Schmiermittelfilm beim Anfahren fast nicht vorhanden oder kann im Betrieb bei hohen Flächenpressungen örtlich zerstört werden. In diesen Fällen wirken die Graphitausscheidungen von Gusseisen als Schmiermittelreservoir. Der bei Ausfall der Schmierung herausgerissene Graphit kann selbst als Schmierstoff wirken und den zum Verschweißen führenden metallischen Kontakt verhindern oder verzögern. In Vergleichsuntersuchungen an Gusseisen, Stahl und Kupfer ließ sich diese Wirkung des Graphits eindeutig nachweisen. Während bei Stahl oder Kupfer bereits Fressen auftrat, wurde die Oberfläche von Gusseisen nur durch plastisches Fließen unter dem Einfluss der Reibungswärme geschädigt [139].
Lamellen- und Kugelgraphit üben die gleiche Wirkung aus, aber die höhere Festigkeit des Gusseisens mit Kugelgraphit setzt die Oberflächenzerstörung herab, wobei vor allem perlitische und auch ferritisch-perlitische Sorten den höchsten Widerstand gegen Gleitverschleiß und Fressen sowohl bei trockener Reibung [140] als auch beim Zusammenbruch des Schmierfilms [141] haben. Während bei der in der Praxis kaum auftretenden reinen Rollbeanspruchung EN-GJS-400-18 und EN-GJS-700-2 gleich beständig sind [140], nimmt bei Gleit-Roll-Verschleiß die Beständigkeit mit steigender Festigkeit zu. Sie ist bei austenitisch-ferritischen Gusseisen mit Kugelgraphit (ADI) am höchsten [142, 143], da es hier zusätzlich infolge des Austenitgehalts zu einer starken Kaltverfestigung der Oberfläche kommen kann.
Im Bild 146 ist die für Zahnradwerkstoffe wichtige Dauerwälzfestigkeit verschiedener Sorten von Gusseisen mit Kugelgraphit im Vergleich zu anderen Gusseisenwerkstoffen und Zahnradstählen dargestellt. Beim Überschreiten der Dauerwälzfestigkeit tritt Grübchenbildung auf. Die Beständigkeit dagegen nimmt mit steigender Festigkeit des Gusseisens mit Kugelgraphit zu. EN-GJS-700-2 und ENGJS-800-2 übertreffen die legierten Zahnradstähle (zum Beispiel 42CrMo4 und 50CrMo4). Austenitisch-ferritische Gefüge erreichen die Werte von gasnitrierten Stählen.
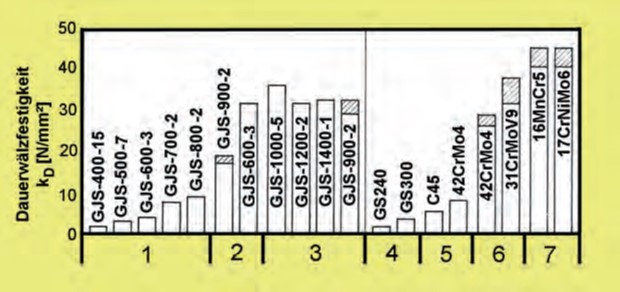
1 - Gusseisensorten nach DIN EN 1564, Normalzustand
2 - Gusseisensorten nach DIN EN 1564, vergütet (links) und induktiv gehärtet (rechts)
3 - ADI-Gusseisen
4 - Stahlguss nach DIN EN 10293
5 - Schmiedestahl, vergütet
6 - Schmiedestahl, gasnitriert
7 - Stahl, einsatzgehärtet
Im Gebiet oberhalb der Wälzfestigkeit bleiben die aufgetretenen Grübchenschäden im Gegensatz zu Stahlzahnrädern verhältnismäßig klein, so dass kurzzeitige Überschreitungen der angegebenen Dauerwälzfestigkeit zu keinen größeren Flankenausbrüchen führen. Das bedeutet auch, dass die Schadenslinie sehr nahe bei der Wöhlerlinie liegt und eine relativ hohe Überlastbarkeit möglich ist. Von besonderem Vorteil für die Dauerwälzfestigkeit ist die im Verhältnis zu vergütetem Stahl geringe Kerbempfindlichkeit der Oberflächen und das bessere Einlaufverhalten der Zahnflanken. Daraus ergibt sich für gefräste Zahnflanken aus Gusseisen mit Kugelgraphit eine relativ hohe Dauerwälzfestigkeit, während bei Stahlzahnrädern die größere Rauheit des Abwälzfräsens zu einer beachtlichen Verringerung der Dauerwälzfestigkeit im Vergleich zur geschliffenen Oberfläche führt [146].
Korrosionsbeständigkeit
Unter Korrosion versteht man die Zerstörung des Werkstoffs durch chemische oder elektrochemische Reaktion mit seiner Umgebung. Die Basis der Korrosion von Eisenwerkstoffen ist die Umwandlung des Eisens in Eisen-Ionen und Elektronen, wobei die Elektronen durch einen Elektronenakzeptor gebunden werden müssen. Ist dies nicht gegeben, was nur bei trockener sauberer Luft und destilliertem Wasser der Fall ist, kommt die Korrosion zum Stillstand [147].
Korrosionsverhalten von Gusseisen
Eine wichtige Rolle für den Korrosionsverlauf spielt der Aufbau von Deckschichten. Bei der Passivierung, wie sie von Edelstählen bekannt ist, tritt keine Korrosion auf. Bei Gusseisen ist unter fast allen Bedingungen keine Passivierung möglich, sondern es bildet sich nur eine Deckschicht, die aber das darunter liegende Metall nicht sicher zu schützen vermag, da sie nicht dicht und fest haftend genug ist. Alle Faktoren, die die Haftung und Haltbarkeit der Deckschicht ändern, beeinflussen auch die Korrosionsbeständigkeit von Gusseisen mit Kugelgraphit. Die Tabelle 14 enthält Anhaltswerte für die Korrosionsgeschwindigkeit von un- und niedrig legierten Gusseisen in verschiedenen Medien.
| Medium | Bedingungen | Abtragsrate [mm/Jahr] |
| Luft | Inland | < 0,250 |
| Küstennähe | < 0,250 | |
| natürliches Wasser | weich | < 0,250 |
| hart | < 0,125 | |
| Seewasser | < 0,250 | |
| verdünnte Säuren und saure Abwässer | < 0,250 | |
| konzentrierte Mineralsäuren | < 0,250 | |
| verdünnte alkalische Lösungen und Abwässer | < 0,125 | |
| konzentrierte Alkalien | < 0,250 |
Die Unterschiede zwischen Gusseisen mit Lamellen- und Kugelgraphit sind nur gering. Die Korrosionsgeschwindigkeit an Luft hängt von der Luftfeuchtigkeit und der Reinheit ab. Ab einer relativen Feuchte von 70 % ist ein Korrosionsangriff möglich, der durch Schwefeldioxid und andere Verunreinigungen, die zu einer leichten Säurebildung führen, beschleunigt wird. Auch Chloride wie in Seeluft beschleunigen die Korrosion.
Die Korrosion in Süßwasser hängt von der Bildung einer schützenden Kruste ab. Hartes Wasser ist weniger aggressiv als weiches Wasser. Mit Ionentauschern enthärtetes Wasser, dessen CO2-Gehalt nicht verändert wurde, kann ziemlich aggressiv wirken [147 - 149]. Bei Kreisläufen von Prozesswasser können Inhibitoren den Korrosionsangriff in erheblichem Maße vermindern.
Sauberes ruhendes Seewasser ist nicht wesentlich aggressiver als Süßwasser, aber Strömung, Verunreinigungen und die Anwesenheit von Sulfat reduzierenden Bakterien können die Korrosionsraten erheblich erhöhen. Häufig kommt es hier auch zu Lochfraß [150].
Eine brauchbare Beständigkeit gegen Säuren oder saure Lösungen besteht nicht. Wässrige alkalische Lösungen greifen dagegen bei Temperaturen unter etwa 70 °C Gusseisen kaum an. Die Korrosionsrate im Boden hängt sehr stark von der Bodenbeschaffenheit ab. Gut gelüftete lockere Böden verursachen eine geringe Korrosion, während nasse Böden und anaerobische Bedingungen die Korrosion verstärken. Der Einfluss des Gefüges auf die Korrosionsbeständigkeit ist gering und schwächer als der von Variationen der oben genannten Einflussgrößen. Gussfehler wirken sich ungünstig aus.
Ein Sonderfall ist die Beständigkeit in Schwefelsäure [147]. Während die Beständigkeit in verdünnter Säure sehr gering ist, tritt bei Säurekonzentrationen über 80 %, vor allem aber über 96 %, ein Beständigkeitsbereich auf, der sich bei den hohen Konzentrationen bis zu über 300 °C erstreckt. Nach Untersuchungen an Gusseisen mit Lamellengraphit [151, 152] sind für eine hohe Beständigkeit eine gleichmäßige feinperlitische Gefügausbildung von Bedeutung, wobei ein niedriger Siliciumgehalt und Zusätze von Kupfer und Nickel günstig wirken.
Legierungselemente in niedrigen Gehalten ändern an den oben genannten Verhältnissen im Prinzip nichts, können aber durch Verstärkung und Verdichtung der Schutzschicht die Korrosionsraten etwas vermindern. Etwa 1 % Kupfer kann die Beständigkeit an Luft sowie in sehr schwach sauren Lösungen verbessern. Nickel in Gehalten von 2 bis 4 % kann die Beständigkeit in entmineralisiertem Wasser steigern und wirkt sich vor allem günstig bei Korrosion durch alkalische Medien aus, wobei die Beständigkeit mit steigendem Nickelgehalt zunimmt. Hier ist ein niedriger Siliciumgehalt vorteilhaft.
Korrosionsermüdung
Unter dem Einfluss von Korrosion können sich die mechanischen Eigenschaften von Gusseisen mit Kugelgraphit ebenso wie bei anderen Werkstoffen verschlechtern. Bereits nach 30 Tagen in leicht bewegtem, luftgesättigtem, destilliertem Wasser wurde eine Verminderung der Zugfestigkeit, der 0,2%-Dehngrenze und der Bruchdehnung von ferritischem, perlitischem und vergütetem Gusseisen mit Kugelgraphit festgestellt [153]. Der Festigkeitsverlust war umso größer, je höher die Härte beziehungsweise die Festigkeit des Eisens waren. Dieser Effekt wird auf eine Wasserstoffversprödung zurückgeführt. Eine ähnliche Schädigung tritt auch bei ADI (siehe Kapitel 8.2) auf.
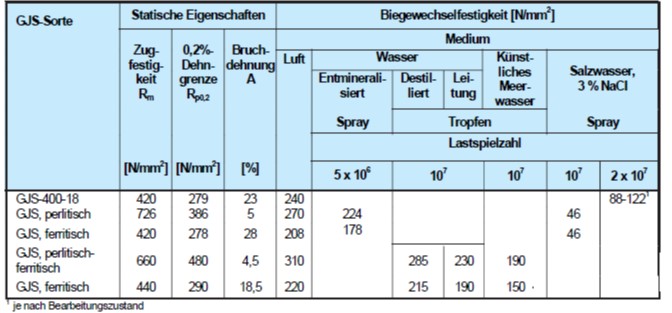
Unter dem Einfluss von Korrosion wird vor allem die Schwingfestigkeit herabgesetzt. Dabei lässt sich oft keine Dauerfestigkeit mehr feststellen, sondern nur eine Zeitfestigkeit, da die Festigkeit mit steigender Lastspielzahl kontinuierlich abfällt. Tabelle 15 enthält einige Versuchsergebnisse. Die Ergebnisse sind allerdings kaum vergleichbar, da die Versuchsbedingungen, die einen sehr starken Einfluss ausüben, bei jeder Versuchsreihe unterschiedlich waren. Durch Inhibitoren lässt sich das Verhalten der Werkstoffe teilweise merklich verbessern [9].
Tabelle 15: Ergebnisse einiger Biegewechselversuche mit ungekerbten Proben in verschiedenen Medien [154 -156]
Bruchmechanische Eigenschaften
Grundlagen
Mit der Anwendung bruchmechanischer Kriterien für die Werkstoffauswahl beziehungsweise Bauteilsicherheitsbewertung werden die konventionellen Kriterien ergänzt und erweitert. Dadurch kann der Konstrukteur über die erstmals mögliche Einbeziehung der Werkstoffzähigkeit, definiert als Werkstoffwiderstand gegen Risseinleitung oder Rissausbreitung, in die Bruchsicherheitsbewertung eine beanspruchungsgerechtere Werkstoffauswahl treffen, als das auf der Basis der Schlagoder Kerbschlagarbeit möglich ist [157].
Voraussetzung ist die Ableitung quantitativer Korrelationen zwischen der Bauteilbeanspruchung, der Größe vorhandener beziehungsweise hypothetisch angenommener Risse oder rissähnlicher Spannungskonzentrationsstellen und der Bruchzähigkeit des Werkstoffs. Hierzu gibt Bild 152 eine schematischen Übersicht. Das Einbeziehen bruchmechanischer Konzepte zur beanspruchungsgerechten Gusswerkstoff- und Gussteilbewertung wird unter Beachtung von Gussfehlern oder denkbarer gießtechnischer Unregelmäßigkeiten vor allem dann erforderlich und zunehmend praktiziert, wenn Gusswerkstoffe aufgrund ihrer spezifischen Vorteile in festigkeitsbeanspruchten und potentiell bruchgefährdeten Konstruktionen zum Einsatz kommen.
Der bruchmechanische Festigkeitsnachweis für Bauteile aus Gusseisenwerkstoffen [158] ist Bestandteil der FKM-Richtlinie [27] und weiterer fachspezifischer Regelwerke [159, 160], wobei auch für diese Bauteile die Bruchsicherheitsbewertung geschweißter Konstruktionen [161] unter Beachtung bestehender Richtlinien [162] zur bruchmechanischen Bewertung zunehmend zu beachten sein wird. Die Anwendung der FKM-Richtlinie ermöglicht die gezielte Lösung folgender Aufgabenstellungen:
- In der Konstruktionsphase können angenommene Fehler bewertet werden, um Geometrie, Werkstoff und Herstellungsverfahren zu spezifizieren;
- Während der Herstellung und im Betrieb sind geeignete zerstörungsfreie Prüfverfahren zur Qualitätskontrolle auszuwählen und gegebenenfalls Inspektionsintervalle festzulegen;
- Während des Betriebes müssen Bauteile mit Fehlern hinsichtlich ihrer gegenwärtigen und zukünftigen Gebrauchseignung bewertet werden, im Schadensfall sind die Schadensursachen zu ermitteln.
Eine wesentliche Voraussetzung für die Anwendung dieses Konzeptes besteht in der Verfügbarkeit bruchmechanischer Kennwerte sowohl für die Berechnung zulässiger Rissgrößen oder Spannungen bei statischer und dynamischer Beanspruchung als auch der Restlebensdauer zyklisch beanspruchter Bauteile. Die FKMRichtlinie beinhaltet eine Datenbank für bruchmechanische Werkstoffkennwerte, die im Ergebnis einer Literaturrecherche entwickelt wurde.
Statische Beanspruchung
Die experimentelle Ermittlung statischer Bruchzähigkeitswerte kann nach DIN EN ISO 127837 [163], ESIS P2-92 [164] oder ISO 12135 [165] erfolgen. Bestimmt werden KIc-Werte nach dem Konzept der linearelastischen Bruchmechanik (ebener Dehnungszustand EDZ) oder Kennwerte des CTOD- und J-Integral-Konzeptes bei elastisch-plastischem Werkstoffverhalten (ebener Spannungszustand ESZ). Eine
Umrechnung von J in K ist über die elastischen Konstanten E und V
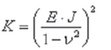
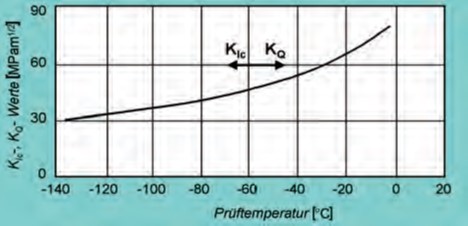
möglich. Aus dem Verlauf der temperaturabhängigen Bruchzähigkeitskennwerte KIc (EDZ) beziehungsweise KQ (ESZ) für ferritisches EN-GJS-400-15, gemessen an 100 bis 200 mm dicken CT-Proben, ist ableitbar, dass gültige, das heißt auf das Bauteil übertragbare bruchmechanische Kennwerte mit vertretbaren Probenabmessungen nur mit fließbruchmechanischen Konzepten bestimmt werden können (Bild 153).
Die gefüge- und damit festigkeitsbedingte Abhängigkeit der Bruchzähigkeit KIcJ, abgeleitet aus Risswiderstandskurven des J-Integral-Konzeptes und Umrechnung in K-Werte nach Gleichung (3) geht aus Bild 154 hervor.
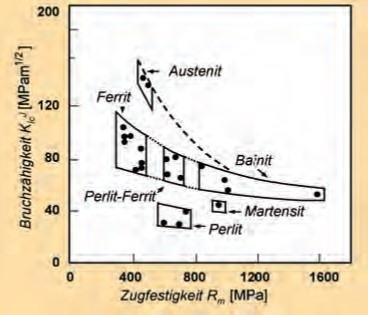
25 mm, Teilentlastungsverfahren, ASTM E 813-81) in Abhängigkeit von der Zugfestigkeit für unterschiedliche Gusseisenwerkstoffe [167]
Die in Tabelle 16 aufgeführten Kennwerte des CTOD- und J-Integral-Konzeptes wurden an 20%-seitengekerbten SENBProben (10 x 20 x 100 mm) über die Aufnahme von Risswiderstandskurven (Compliance Methode) gemäß ESIS P2-92 bestimmt. Die physikalischen Rissinitiierungswerte JiBL und δiBL- werden im Schnittpunkt der Blunting-Line mit der JR-bzw. δR-Kurve ermittelt. Die Umrechnung der JiBL-Werte in Werte des K-Konzeptes erfolgt nach Gleichung (3).
Tabelle 16: Mechanische und bruchmechanische Kennwerte n. b. nicht bestimmt
| Werkstoff EN- … | Rp0,2 [N/mm²] | Rm [N/mm²] | A [%] | HB | KV [J] | SB [mm] | JiBL [kJm-2] | J0,2 [kJm-2] | KIcJi [N/mm² ¬m] | δiBL [μm] | δ0,2 [μm] |
| GJS-400-15 | 246 | 413 | 26 | 143 | 18 | 0,46 | 21 | 51 | 60 | 37 | 92 |
| GJS-800-10 | 637 | 893 | 13 | 292 | n.b. | n.b. | 11 | 35 | 45 | 31 | 27 |
| GJS-1000-5 | 800 | 1062 | 8 | 344 | 7 | 0,03 | 8 | 20 | 37 | 6 | 15 |
Die Bauteilübertragbarkeit bruchmechanischer Kennwerte, das heißt die Berechnung zulässiger Fehlerabmessungen, setzt die Unabhängigkeit der ermittelten Werte von Probengröße und -geometrie voraus. Vorliegende Ergebnisse zur Bauteilübertragbarkeit fließbruchmechanischer Kennwerte des J-Integral- Konzeptes bestätigen, dass physikalische Rissinitiierungswerte nach der hier erfolgten Art der Auswertung die Forderung weitestgehend erfüllen. Die auch praktizierte Bestimmung der technischen Rissinitiierungswerte J0,2 und δ0,2 erfolgt über die JR- bzw. δR-Kurven bei einem Betrag der stabilen Rissausbreitung von Δa = 0,2 mm. Aus den bruchmechanischen Kennwerten für unterschiedliche Gusseisenwerkstoffe gemäß Tabelle 16, in die auch die mechanischen Kennwerte des Zugversuchs, die Brinellhärte HB und die Kennwerte des Kerbschlagbiegeversuchs (Kerbschlagzähigkeit KV, Seitliche Breitung SB, ISO-V-Probe) aufgeführt sind, folgt, dass bei Raumtemperatur in der duktilen Matrix das Werkstoffversagen über eine stabile Rissausbreitung
beginnt.
Wird die Sorte EN-GJS-600-3 mit überwiegend perlitischem Gefüge in diese Betrachtung mit einbezogen, so wird hier das Werkstoffversagen durch eine überwiegend spaltflächige stabile Rissausbreitung bis zu einem deutlichen „pop-in“- Effekt eingeleitet, dem instabile Rissausbreitung folgt. Die für EN-GJS-600-3 definierten Jc = 15 kJm-2 und δc =21 μm charakterisieren einen kritischen Rissinitiierungswert bei Auftreten des „pop-in“-Effektes, das heißt einer lokalen instabilen Rissausbreitung, der bei weiterer Belastung Werkstoffversagen durch instabile Rissausbreitung folgt.
Die FKM-Richtlinie verweist auf die Möglichkeit, bruchmechanische Kennwerte über Korrelationen zu anderen Kennwerten oder dem Gefüge abzuschätzen. Aus vorliegenden Ergebnissen folgt, dass eine Abschätzung physikalischer Rissinitiierungswerte von ferritischen Gusseisenwerkstoffen über Gefügeparameter und Kennwerte des Zugversuchs möglich ist. Für ferritisches Gusseisen mit globularer und vermicularer Graphitausbildung folgt die nach Bild 155 empirisch abgeleitete Korrelation
Ji = 4,6 (Rp0,2 . A . λ) + 11,3 kJ/m2 (4)
und für den Fall, dass im Ergebnis gießtechnisch bedingter größerer Abweichungen der Graphitteilchen von der Kugelform die Risseinleitungszähigkeit Ji durch die innere Kerbwirkung der Teilchen deutlich herabgesetzt ist, wie beispielsweise bei vermicularer Graphitausbildung, die modifizierte Beziehung
Ji = 4,2 · 105 · kJ/m3 (f . λ) + 9,4 kJ/m2 (5)
Hierin bedeuten λ der mit der Teilchenzahl und der Teilchengröße korrespondierende mittlere Graphitteilchenabstand und f der Formfaktor f = 4 π . AT/U2 ≤ 1, wobei AT den Flächeninhalt und U den Umfang der Schnittfläche des Graphitteilchens beschreiben und sich für kugelförmige Teilchen f = 1 ergibt [168].
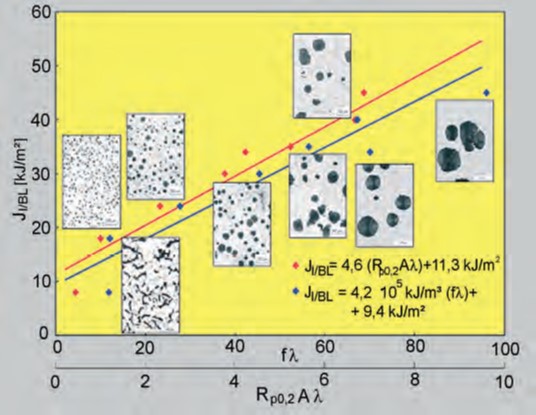
Hinsichtlich des Einflusses von Gefügeabweichungen (unterschiedliche Nodularität, interzellularer Graphit, Zellgrenzencarbide) auf die bruchmechanischen Eigenschaften von EN-GJS-400-15 und ENGJS-700-2 soll hier auf [169] verwiesen werden. Große Anteile von Chunky-Graphitentartung führen, wie aus [170] hervorgeht, neben einer deutlichen Verringerung der Festigkeit und Verformbarkeit, auch zu einer beträchtlichen Verminderung des Risseinleitungs- und Rissausbreitungswiderstandes von EN-GJS-400-15.
Mit dem gestiegenen Einsatz der Gusseisenwerkstoffe mit globularer Graphitausbildung hat auch die Schweißeignung dieser Werkstoffgruppe an Bedeutung gewonnen. Bei der Herstellung artgleicher Schweißverbindungen aus ferritischem Gusseisen EN-GJS-400-15, gekoppelt mit einer „insitu“-Wärmebehandlung nach dem Absetzen der Decklage aus der Schweißwärme, wurde erkannt, dass bei Übereinstimmung der mechanischen Eigenschaften von Grundwerkstoff und Wärmeeinflusszone ein deutlicher Unterschied zum Schweißgut auftritt, der in der erstarrungsbedingten, um den Faktor 10 höheren Graphitteilchenanzahl je mm2 begründet ist [171]. Die partielle Bruchgefahr, die von einem derartigen zähigkeitsmindernden Mismatch-Effekt ausgeht, wird verstärkt, wenn die mögliche Stützwirkung duktiler Nachbarbereiche durch das Auftreten spröder Gefügeanteile in der Wärmeeinflusszone unterdrückt wird. Aus vorliegenden Ergebnissen folgt, dass mit dem abkühlungsbedingten Auftreten perlitischer, bainitischer und martensitischer Gefüge in der ferritischen Matrix der Rissausbreitungswiderstand bei unterschiedlichen Beanspruchungsarten deutlich verringert wird, so dass sowohl der Anteil dieser Gefüge als auch ihre mögliche Anordnung bei der Optimierung der Schweißtechnologie vordergründig zu beachten sind.
Für eine umfassende Bewertung des Festigkeits- und Zähigkeitsverhaltens hochfester ADI-Werkstoffe (siehe 8.2) ist neben der Kenntnis der mechanischen Eigenschaften auch die Einbeziehung bruchmechanischer Kennwerte (Tabelle 16) erforderlich, wenn der Einsatz in sicherheitstechnisch relevanten Gussteilen erfolgt.
Zyklische Beanspruchung
Im Rahmen umfassender Betriebsfestigkeitsanalysenkommen bruchmechanische Rissfortschrittskonzepte sowohl zur gefügeabhängigen Bewertung des Rissausbreitungsverhaltens als auch zur Berechnung der Bauteillebensdauer zum Einsatz. Eine wesentliche Voraussetzung hierfür ist die Verfügbarkeit der bruchmechanischen Kennwerte unter Zugrundelegung der da/dN-ΔK-Kurven (Bild 157).
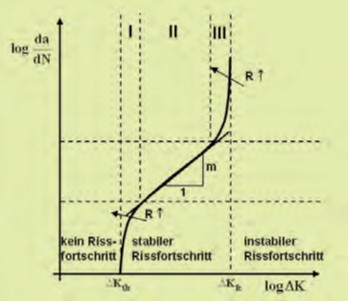
Die Messung der Risswachstumsgeschwindigkeit da/dN (N Lastspiel) in Abhängigkeit vom zyklischen Spannungsintensitätsfaktor ΔK wurde über die rechnergesteuerte Messung der Resonanzfrequenz als Maß für die von der Risstiefe abhängige Probennachgiebigkeit vorgenommen. Bei der hier erreichten Auflösung von etwa 2 μm ist für den Bereich I der da/dN-ΔK-Kurve die exakte Bestimmung des Schwellenwertes ΔKth möglich. Dieser hat die Bedeutung einer bruchmechanischen Dauerfestigkeit, das heißt bei ΔK < ΔKth tritt kein Risswachstum auf. Die Ermittlung der werkstoffabhängigen Konstanten m und C der Paris-Erdogan-Gleichung (Bereich II der da/dN-ΔK-Kurve)
da/dN = C [ ΔK]m (6)
als Basis für das Abschätzen der Restlebensdauer fehlerbehafteter Gussteile erfolgt in Anlehnung an ASTM E647-86 [172].
In der Tabelle 17 sind die bruchmechanischen Kennwerte in Abhängigkeit von der Mittelspannung (R-Wert) unter Einbeziehung des den Restbruch charakterisierenden ΔKfc-Wertes (Bereich III der da/dN-ΔK-Kurve) zusammengestellt, wobei die Kennwerte der da/dN-ΔK-Kurve die Mittelwerte von je drei SENB-Proben der Abmessung 10 x 20 x 100 mm sind. Die Auswertung des Streufeldes von fünf Proben des EN-GJS-400-15 ergab für einen Mittelwert des ΔKth-Wertes von 7,5 N/mm²¬m eine Standardabweichung von ± 0,4 N/mm²¬m, die in dieser Höhe durch die Gesamtheit der Versuche bestätigt wird. Der relative Fehler liegt in Übereinstimmung mit Messungen an Stahl im Bereich von ± 10 % [173].
Tabelle 17: Bruchmechanische Kennwerte der zyklischen Risswachstumskurve
| Werkstoff EN- … | R-Wert | ΔKth [N/mm²¬m] | m | C | ΔKfc [N/mm² m] |
| GJS-400-15 | 0,1 0,3 0,5 | 7,5 6,2 4,5 | 4,5 4,6 4,2 | 2,2·10-10 3,8·10-10 1,3·10-9 | 40 31 22 |
| GJS-600-3 | 0,1 0,3 0,5 | 6,9 6,6 4,6 | 4,5 4,6 4,2 | 1,2·10-9 1,3·10-9 1,9·10-9 | 34 27 19 |
| GJS-800-10 | 0,1 0,3 0,5 | 5,4 4,8 4,3 | 2,9 3,0 3,2 | 0,9·10-8 1,1·10-8 1,0·10-8 | 51 40 29 |
| GJS-1000-5 | 0,1 0,3 0,5 | 5,5 4,0 3,4 | 2,9 2,7 2,8 | 2,3·10-8 3,3·10-8 3,9·10-8 | 45 33 24 |
Aus Untersuchungen an ferritischem ENGJS-400-15 mit unterschiedlicher Graphitteilchengröße (dG = 21 bis 54 μm) folgt, dass mit abnehmender Graphitteilchengröße die ΔKth-Werte kleiner werden. Dies korreliert einerseits mit der korrespondierenden Abnahme des Teilchenabstandes λ und der hieraus nach dem Ritchie-Modell folgenden Abnahme der freien Weglänge der Versetzungen sowie andererseits mit der Zunahme der 0,2-Dehngrenze.
Beide Einflussgrößen verringern die zur Rissbildung erforderliche plastische Deformation, zum Beispiel in Ermüdungsgleitbändern oder an Grenzflächen der Graphitteilchen, wie bei „in-situ“-Versuchen im REM beobachtet wurde [174]. Die bei R = 0,1 ermittelten ΔKth-Werte von mehr als 6 N/mm² ¬m stimmen mit Messungen in [175] an EN-GJS-400-15 (Rp0,2 = 299 N/mm², ΔKth = 7,3 N/mm²¬ m) überein und liegen oberhalb der Werte für Stahl vergleichbarer Festigkeit. Als Ursache kann die teilchenbedingte Behinderung der plastischen Deformation angeführt werden.
Für den Bereich II der da/dN-ΔK-Kurve ist ein weitestgehend Teilchengrößen unabhängiges Risswachstum zu verzeichnen. Erst bei Graphitteilchengrößen dG = 12 μm im Schweißgut artgleicher Schweißverbindungen aus EN-GJS-400-15 ist ein deutlich höheres Risswachstum zu verzeichnen [173]. Für Graphitteilchengrößen im Bereich von dG = 21 bis 54 μm kann als Mittelwertskurve
da/dN = 6,4 x 10-12 (ΔK)6,1 (7)
angegeben werden.
Im Rahmen von „in-situ“-Versuchen wurde nachgewiesen, dass die Schädigungsprozesse bei globularer Graphitausbildung durch Ablösen der Graphitkugeln von der ferritischen Matrix mit nachfolgender Mikrorissbildung bestimmt werden. Abweichungen von der globularen Graphitausbildung führen, wie Untersuchungen an Gusseisen mit vermicularer Graphitausbildung (GJV-300) zeigen, infolge des Brechens der Graphitteilchen und Mikrorissbildung, zu höheren Risswachstumsgeschwindigkeiten. Chunky-Graphit im EN-GJS-400-15 bewirkt ebenfalls aufgrund der hohen inneren Kerbwirkung eine deutliche Erhöhung der da/dN-Werte im Bereich II der da/dN-ΔK-Kurve [170].
Aus einer vergleichenden Bewertung des zyklischen Risswachstums im Bereich II der da/dN-ΔK-Kurven folgt für Gusseisen mit globularer Graphitausbildung und ferritischem, ferritisch-perlitischem und austenitisch-ferritisches Grundgefüge eine weitgehende Gefügeunabhängigkeit [173]. Dagegen folgt aus Tabelle 17 für den Bereich I die bekannte Abhängigkeit der ΔKth-Werte von der Mittelspannung (R-Wert) und in Hinblick auf die Gefüge die Verringerung von ΔKth mit zunehmender Rp0,2-Grenze.
Die Abhängigkeit von der Mittelspannung wird auch für den ΔKfc-Wert (Bereich III) deutlich, der den Übergang zum Restbruch charakterisiert. Die höheren ΔKfc-Werte der ADI-Werkstoffe EN-GJS-800-10 und EN-GJS-1000-5 im Vergleich zu EN-GJS-600-3 deuten, wie auch aus LCFund Randomversuchen folgt, auf eine höhere Überlastbarkeit hin. Über den Vergleich des Bruchverhaltens dieser ADI-Werkstoffe mit dem Radstahl R7 können Fragen hinsichtlich der möglichen Substitution von Vergütungsstählen in Verbindung mit der hohen Verschleißbeständigkeit und den besseren Dämpfungseigenschaften beantwortet werden.
Dabei ist zu beachten, dass für eine Restlebensdauerberechnung belastbare Informationen zum Risswachstumsverhalten notwendig sind. In der Designphase werden für derartige bruchmechanische Sicherheitsanalysen häufig konservative Referenzkurven verwendet, die als obere Hüllkurven über eine Vielzahl von Messergebnissen einer Werkstoffgruppe abgeleitet wurden. Dabei ist nicht immer ersichtlich, wie groß die Sicherheitsmarge im Einzelfall ausfällt.
Eine statistische Auswertung ist über die Ableitung von Quantitrisswachstumskurven auf der Basis des NASGRO-Computercodes möglich, der als ESACRACK 4.0 [176] verfügbar ist.
Dynamische Beanspruchung
Bei einer umfassenden Bewertung der Bauteilsicherheit, insbesondere für Unfallszenarien bei denen infolge stoßartiger Belastungen schnelle Änderungen des Spannungs- und Deformationszustandes auftreten, kann die Beanspruchbarkeit des Werkstoffs im Bauteil mit bruchmechanischen Werkstoffkennwerten charakterisiert werden. Für die experimentelle Bestimmung dynamischer Bruchzähigkeitswerte stehen hinsichtlich des Regelwerkes nur erste Ansätze zur Verfügung [178] bis [179], die sich an die Standards für den statischen Belastungsfall anlehnen. Vorliegende Ergebnisse für EN-GJS-400-15 orientieren sich schwerpunktmäßig an der Bruchsicherheitsbewertung von Behältern für den Transport abgebrannter Brennstäbe (Bild 158). Untersuchungen an EN-GJS-400-15 mit erhöhtem Perlitanteil im Temperaturbereich von RT bis - 50°C an stoßbiegebeanspruchten (K ≈ 5 ·104 N/mm²¬ m/s) SENB-Proben (Dicke 140 mm) zeigen, dass bei - 40° C probendickenunabhängige KId-Werte im Bereich von 50 bis 60 N/mm²¬m vorliegen.

Die experimentelle Bestimmung dynamischer Bruchzähigkeitskennwerte mit vertretbaren Probenabmessungen wird über die Aufnahme dynamischer Risswiderstandskurven nach dem CTOD- oder JIntegral-Konzept praktiziert, wobei die Zeit und Material aufwändige Mehrprobentechnik („low-blow“-Technik) zum Einsatz kommt. Bild 159 enthält die Bestimmung und Definition physikalischer (Jdi) und technischer (Jd0,2) Rissinitiierungswerte am Beispiel eines ADI-Werkstoffs, ermittelt an gestuft schlagbiegebeanspruchten SENB-Proben (10 x 10 x 55 mm) mit Ermüdungsriss („low-blow“-Technik). Für die Entwicklung von rationelleren Einprobenverfahren [180, 181] zum Ermitteln dynamischer Risswiderstandskurven für Gusseisen gibt es gegenwärtig Vorschläge mit unterschiedlichem Aufwand und Erfolg.
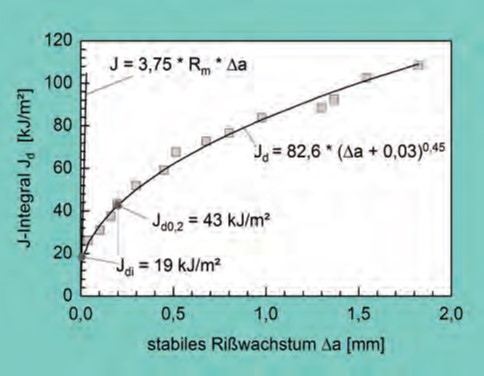
Die dynamischen Rissinitiierungswerte für ferritisches EN-GJS-400-15 zeigen in Analogie zu den statischen Werten eine deutliche Gefügeabhängigkeit und machen im direkten Vergleich deutlich, dass die stoßartige Beanspruchung sowohl bei RT als auch bei tiefen Temperaturen zu einer deutlichen Verringerung des Risseinleitungswiderstandes führt [182]. Bestätigt wird dies auch im Ergebnis der ruchmechanischen
Bewertung einer artgleichen Schweißverbindung aus EN-GJS-400-15 bei statischer und dynamischer Beanspruchung [183]. Hier ist vor allem der zähigkeitsverringernde Einfluss kleiner Graphitteilchen im Schweißgut und erhöhter Perlitanteile auf den Risseinleitungswiderstand der Schweißverbindung bei dynamischer Beanspruchung in Verbindung mit dem Werkstoffverhalten bei tiefen Temperaturen zu beachten.
Auf den Einfluss dynamischer Beanspruchungen hinsichtlich des Risseinleitungsund Rissausbreitungswiderstandes duktiler Gusseisenwerkstoffe wird auch in [184 - 186] hingewiesen und auf den zusätzlich zähigkeitsverringernden Einfluss tiefer Umgebungstemperaturen und großer Bauteildicken in [187, 188] aufmerksam gemacht. Beachtenswert sind in diesem Zusammenhang auch Untersuchungen [189, 190] zur Bestimmung der Rissauffangzähigkeit KIa nach ASTM E1221-88 zur Bewertung des temperaturabhängigen Rissstopp-Verhaltens (Rissarrest) von EN-GJS-400-15 (Bild 160).
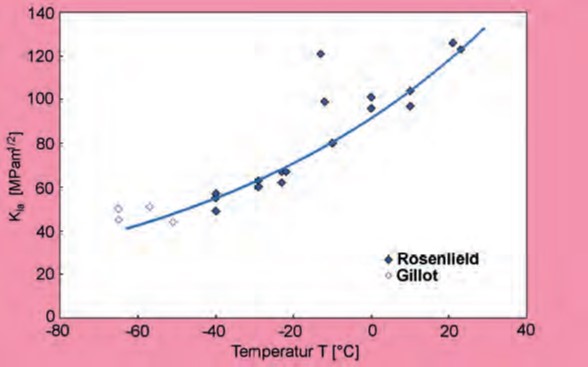
Die bisher praktizierte Anwendung bruchmechanischer Kennwerte im Rahmen der Berechung zulässiger Fehlerabmessungen in Gussteilen macht im direkten Vergleich mit Stahl oder Stahlguss deutlich, dass duktiles Gusseisen in Bezug auf seine Sprödbruchsicherheit höher zu bewerten ist, als es die relativ niedrige Kerbschlagzähigkeit erwarten lässt (Bild 161), wie zum Beispiel aus Untersuchungen im Rahmen der Werkstoffzulassung von duktilem Gusseisen für Schleudergussrohre folgt [191].

In Umsetzung bruchmechanischer Untersuchungsergebnisse konnten 1985 bei der Neufassung des AD-Merkblattes W3/2 die für ferritische Gusseisensorten mit Kugelgraphit im Druckbehälterbau festgelegten Sicherheitsbeiwerte von S = 3,5 auf 2,4 bei Auslegung gegen die 0,2 %-Dehngrenze verringert werden. Für den Transport und die Lagerung radioaktiver Abfälle kommen in Deutschland überwiegend Behälter aus duktilem Gusseisen (Bild 158) mit Kugelgraphit zurAnwendung, für die umfassende Bruchsicherheitsbewertungen unter Einbeziehung bruchmechanischer Festigkeitsberechnungen erforderlich sind. Während bis 2002 ausschließlich die bruchmechanische Bewertung auf der Basis des statischen Belastungsfalles erfolgte, sieht die überarbeitete Leitlinie der Bundesanstalt für Materialforschung und -prüfung (BAM) auch die Einbeziehung stoßartiger Beanspruchungen vor [159]. Gegenstand laufender Untersuchungen sind sowohl die numerische Beanspruchungsanalyse der Behälter unter Einbeziehung hypothetischer Gussfehler [192, 193] als auch die Bestimmung dynamischer Bruchzähigkeitskennwerte in Abhängigkeit von der Prüftemperatur und dem Gussgefüge des EN-GJS-400-15 [194].
Als ein weiteres Beispiel für die Anwendung bruchmechanischer Bemessungsverfahren kann die Planung und der Bau einer Turbinenrohrleitung aus duktilen Gussrohren angeführt werden [195]. Beim Bau eines 16-MW-Laufkraftwerks im Vorarlberg führten besonders hohe Sicherheitsanforderungen und schwierige Einbaubedingungen in alpinem Gelände zu der Entscheidung, die Turbinenleitung im Nennweitenbereich bis DN 1600 bei Betriebsdrücken über 30 bar nicht mit geschweißten Stahlrohren, sondern mit duktilen Schleudergussrohren aus optimiertem EN-GJS-400-15 zu bauen. Die bruchmechanische Bewertung erfolgte auf Basis des „Leck-vor-Bruch“-Kriteriums nach Ermittlung der bruchmechanischen Kennwerte [196]. Im Ergebnis der durchgeführten bruchmechanischen Sicherheitsbewertungen, gestützt durch Berstversuche an der Technischen Versuchs- und Forschungsanstalt der TU Wien, erfolgte die Verwendung von Schleudergussrohren.
Die Anwendung bruchmechanischer Bewertungskonzepte bei der Entwicklung von Eisenbahnrädern aus austenitischferritischem Gusseisen (ADI) erfolgte auf der Basis numerischer Beanspruchungsanalysen. Zur sicherheitstechnischen Auslegung des ADI-Rades (Rp0,2 = 637 N/mm², Rm = 893 N/mm²) gegen Gewaltbruch und Ermüdungsrisswachstum wurde eine linear-elastische bruchmechanische Analyse für hypothetische rissartige Fehler an exponierten Stellen durchgeführt [197]. Aus den berechneten bruchmechanisch relevanten Risslängen kann im Zusammenhang mit wiederkehrenden betrieblichen Überwachungsmaßnahmen und Sicherheitskonzepten eine zulässige Rissgröße abgeleitet werden. Die hier ermittelten kritischen Rissgrößen können mittels zerstörungsfreier Prüfverfahren sicher und zuverlässig diagnostiziert und die Eignung von ADI als alternativer Radwerkstoff bestätigt werden [198] (Bild 162).

Abschließend soll auf die jetzt im Vorschriftenwerk [165] integrierte bruchmechanische Beanspruchungsanalyse potenzieller Ermüdungsbrüche von Komponenten aus EN-GJS-400-18LT in Windenergieanlagen hingewiesen werden, um Schadensfälle zu vermeiden beziehungsweise die Rissausbreitungsgeschwindigkeit in die umfassende Betriebsfestigkeitsanalyse einzubinden [199] (Bilder 163 und 164).


Betriebsfestigkeit
Betriebsfestigkeit ist der Oberbegriff für ein Spektrum von Beanspruchungen, das ein Bauteil während der ihm zugedachten Lebensdauer ohne Versagen ertragen muss. Wesentliche Parameter sind der Werkstoff, die Gestaltung (Bauteilgeometrie), Fertigung (Gießen, Schmieden, Schweißen, Oberflächen- oder Randschichtnachbehandlungen) und Belastung (zum Beispiel mechanisch mit überlagertem Umwelteinfluss) [200- 202]. Die Kosten sind letztendlich dafür verantwortlich, dass Produkte nicht optimal, sondern optimiert auf den Markt kommen (Bild 165). Trotz jahrzehntelanger Forschungsaktivitäten ist eine Freigabe von Sicherheitsbauteilen auf Basis eines rein numerischen Betriebsfestigkeitsnachweises nicht möglich. Sowohl verkürzte Entwicklungszeiten bei gleichzeitig zu gewährleistender Zuverlässigkeit des Produkts als auch die Komplexität und Funktionsintegration bei Baugruppen fordern aber verstärkt deren numerische Behandlung, um zukünftige Entwicklungsprozesse kompetent begleiten zu können. Die Methodenentwicklung zur Erweiterung der Grundlagen zur Gestaltung, Dimensionierung und Optimierung erstreckt sich hierbei auf Parameter wie Fertigung, Randschichtzustand, Größeneinfluss und Festigkeitshypothesen. Die Übertragbarkeit von Schwingfestigkeitskennwerten auf Bauteile ist eng mit lokalen Werkstoff- und Gefügeeigenschaften und auch Versagensmechanismen verknüpft und bedingt dadurch die Unterstützung von Metallographie und Rasterelektronenmikroskopie.
Das heutige Verständnis zur Betriebsfestigkeit hebt sich von der ursprünglich von Ernst Gaßner 1939 eingeführten Definition, dem Festigkeitsverhalten unter zeitlich veränderlichen (variablen) Belastungsbeziehungsweise Beanspruchungsamplituden ab. Sie umfasst - Sonderbelastungen wie Überlasten, die zum Beispiel die Formdehngrenze des Bauteils ansprechen (beispielsweise an Fahrwerkskomponenten beim langsamen Überfahren eines Hindernisses), Beulen oder Knicken einer Struktur und Missbrauch durch dynamische Belastung (Impactbelastung mit hoher Geschwindigkeit und Energie, zum Beispiel beim schnellen Überfahren eines Schlagloches), wobei ein verformungsloser Sprödbruch durch Konstruktion und Werkstoffauswahl ausgeschlossen sein muss. Das heißt, ein duktiler Bruch wäre noch zulässig.
- Kriechbelastungen wie zum Beispiel bei Turbinenschaufeln unter hoher Temperatur und Fliehkraft.
- Verschleiß bei Reibpaarungen, zum Beispiel an Zahnrädern.
- Zyklische Belastungen (Schwingfestigkeit) mit konstanten oder variablen Amplituden mit überlagerten montage- oder belastungsbedingten Mittelwerten können zur Werkstoffermüdung, Rissinitiierung und somit zum Versagen von Bauteilen führen. Das Festigkeitsverhalten unter konstanten Amplituden wird durch die Wöhlerlinie und unter variablen Amplituden durch die Gaßnerlinie beschrieben (Bild 166). Die Wöhlerlinie wird in die Bereiche Kurzzeitfestigkeit (elasto-plastische Beanspruchungen mit größerem plastischem Anteil, definiert bis 5·104 Schwingspiele), Zeitfestigkeit (elasto-plastische Beanspruchungen, Lebensdauer zwischen 5·104 und 2·106 Schwingspielen) und sogenannte „Dauerfestigkeit“ (makroskopisch elastische Beanspruchungen bei Lebensdauern größer als 2·106 Schwingspielen) unterteilt. In diesem Bereich muss mit einem kontinuierlichen, werkstoff-, fertigungs- und umgebungsabhängigen Abfall der Schwingfestigkeit gerechnet werden. Das heißt, es existiert keine Dauerfestigkeit [203]. Die Gaßnerlinie kann sich zwischen 104 und mehr Schwingspielen erstrecken, wobei die Belastungsvorgänge deterministisch oder stochastisch auftreten können. Typische Bauteile im Bereich der Kurzzeitschwingfestigkeit sind Reaktordruckbehälter, der Zeitfestigkeit Türscharniere von Fahrzeugtüren, der sogenannten Dauerfestigkeit Zahnräder, Kurbelwellen oder Pleuel. Typische Komponenten, die gegen variable Betriebsbelastungen bemessen werden, sind Fahrwerksteile, wie Räder, Lenker, Vorder- und Hinterachsträger oder Achsschenkel.
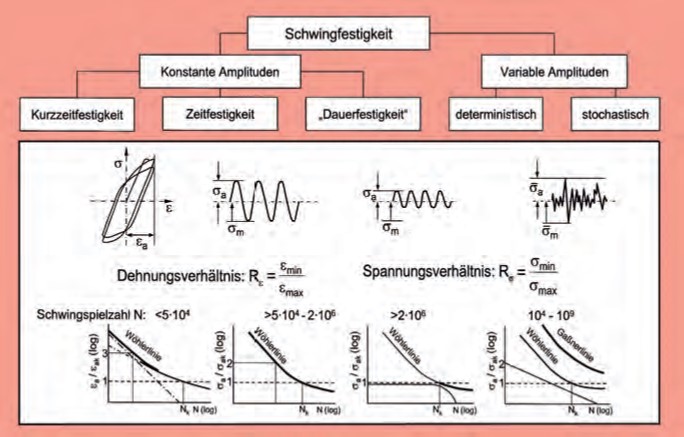
Die beschriebenen Belastungsarten (Sonderbelastung, Kriechen, Verschleiß, Schwingbelastung) treten im Betrieb selten einzeln auf. Sie können durchaus nacheinander oder gemeinsam auftreten, so dass ihre Lebensdauer bestimmende Interaktion stets beachtet werden muss.
Belastungen und Beanspruchungen mit nur konstanten Amplituden, sei es im Bereich der Kurzzeitschwingfestigkeit, der Zeitfestigkeit oder der sogenannten Dauerfestigkeit treten hingegen sehr selten auf. Im Betrieb liegt meistens eine Mischung aus Amplituden unterschiedlicher Höhe vor, die mit dem Begriff Kollektiv (Häufigkeitsverteilung von Amplituden) beschrieben wird und deren Kenntnis für das Ermitteln der zutreffenden Gaßnerlinien Voraussetzung ist.
Einflussgrößen auf die Betriebsfestigkeit
Werkstoff
Bei metallischen Werkstoffen geht in aller Regel mit einer Erhöhung der statischen Festigkeitskennwerte auch ein Erhöhen der Schwingfestigkeit einher. Allerdings trifft dies auch bei Gusswerkstoffen nur für ungekerbte oder schwach gekerbte Bauteilbereiche zu. Ab einer bestimmten Kerbschärfe kann durch eine Steigerung der Zugfestigkeit mit Hilfe einer entsprechenden Legierung oder Wärmebehandlung die Schwingfestigkeit nicht mehr angehoben werden (Bild 167).
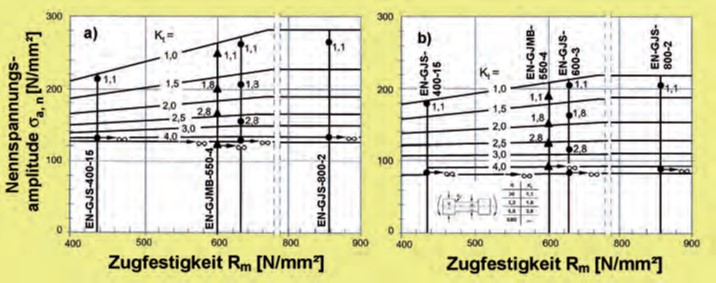
a) bei Wechselbelastung (R = -1)
b) bei Schwellbelastung (R = 0)
Belastungsart: Planbiegung, Oberfläche: feingedreht, Rz = 10 μm, N = 2 . 106, PÜ = 50 %
Folglich ist die höhere Festigkeit eines Werkstoffes nur dann ausnutzbar, wenn Spannungskonzentrationen konstruktiv, zum Beispiel durch größere Radien, abgebaut werden. In Fällen, in denen ein Abbau der Spannungskonzentration konstruktiv nicht möglich ist, können mechanische oder thermo-chemische Oberflächenbehandlungsverfahren nachgeschaltet werden, wobei Werkstoffe mit höheren Festigkeiten bzw. Streckgrenzen, wegen ihrer Fähigkeit entsprechend höhere Druckeigenspannungen aufzubauen, auch größere Steigerungen in der Schwingfestigkeit erfahren als Werkstoffe mit geringeren Festigkeiten [204].
Eine weitere wichtige Kenngröße für die Bemessung von Gussbauteilen ist die Mittelspannungsempfindlichkeit M, die zur Beurteilung des Einflusses von montageoder belastungsbedingten Mittelspannungen auf die ertragbare Schwingfestigkeit dient (Bild 168).
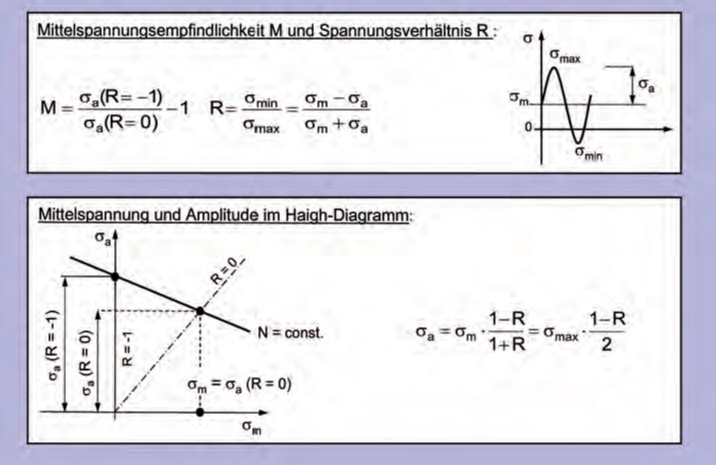
Sie beschreibt das Verhältnis der unter Wechselbelastung (R =-1) und Schwellbelastung (R = 0) ertragbaren Spannungsamplitude σa für einen Werkstoff. Sie liegt bei Gusseisen überwiegend zwischen M = 0,25 ferritische Matrix) und M = 0,50 (perlitische Matrix) und hängt somit auch von der Werkstofffestigkeit ab. Zugmittelspannungen σm mindern bei allen metallischen Konstruktionswerkstoffen die ertragbare Spannungsamplitude σa, Druckmittelspannungen erhöhen sie. Wenn in der Praxis auftretende Spannungsverhältnisse von reiner Wechselbelastung (R = -1) oder Schwellbelastung (R = 0) abweichen, können die zur jeweiligen Mittelspannung gehörigen Schwingfestigkeitsamplituden durch Inter- bzw. Extrapolation näherungsweise aus einem Haigh-Diagramm abgeleitet werden (Bild 189), wobei für Kennwerte außerhalb des Bereiches -1 ≤ R ≤ 0 ein Nachweis empfohlen wird.
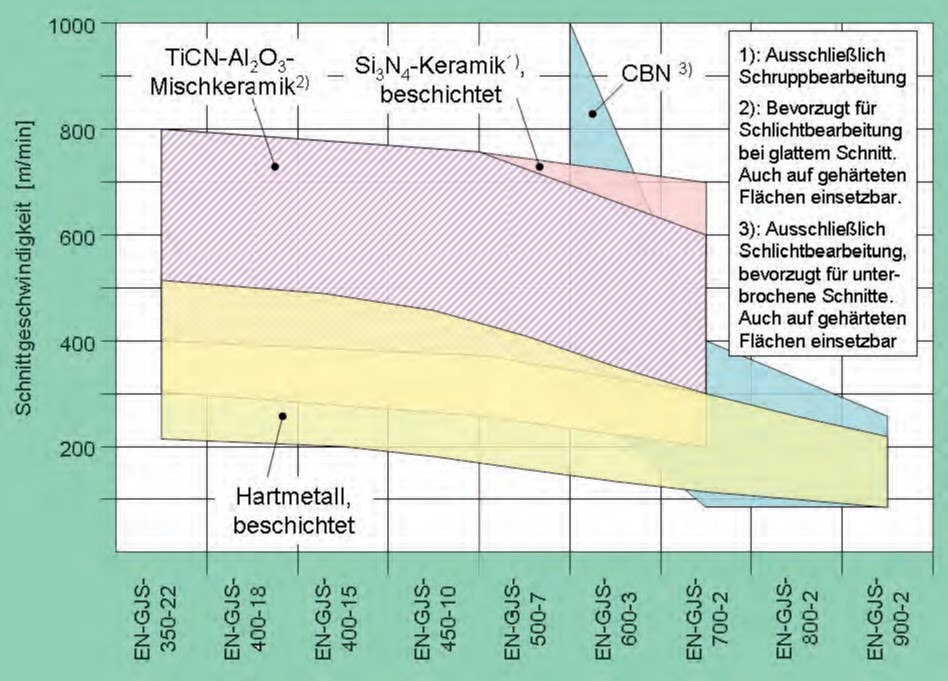
Geometrie, Formgebung
Die Formgebung und damit oftmals verbundene konstruktiv bedingte Kerben beeinflussen die Schwingfestigkeit maßgeblich. Durch das Einbringen von Kerben und mit zunehmender Kerbschärfe (zum Beispiel Absätze, Bohrungen) verringert sich die ertragbare äußere Belastung. Bei sehr scharfen Kerben kann die Schwingfestigkeit einer Konstruktion nicht mehr durch die Wahl eines höherfesten Gusswerkstoffes angehoben werden (Bild 167).
Aufgrund der inneren Kerben, die bei Eisengusswerkstoffen durch den eingelagerten Graphit vorliegen, ist die relative Minderung der Schwingfestigkeit durch bearbeitungsbedingte Kerben niedriger als bei gewalzten oder geschmiedeten Stählen. Die im Vergleich zu Stählen gefügebedingte geringere Kerbempfindlichkeit von Gusswerkstoffen führt im gekerbten Zustand teilweise zu einem mit Stählen vergleichbaren Schwingfestigkeitsverhalten. Dies ermöglicht in Verbindung mit den Gestaltungsfreiräumen der Gusstechnik auch bei hoch belasteten Bauteilen Werkstoffsubstitutionen.
Fertigung
Aufgrund der Reaktion der Schmelze während des Gießprozesses mit den Formwerkstoffen oder bei Vorgängen während der Erstarrung können sich an der Gussoberfläche und im oberflächennahen Bereich Verunreinigungen, Mikroporen oder Zonen mit Gefügeentartungen bilden. Gegenüber dem fein gedrehten oder geschliffenen Oberflächenzustand kann der Gusszustand eine um etwa 20 % niedrigere Schwingfestigkeit aufweisen. Durch eine Oberflächenverfestigung, beispielsweise durch Reinigungsstrahlen, kann gegenüber dem Gusszustand eine Schwingfestigkeitserhöhung um rund 30 % erreicht und somit auch die Rauheit kompensiert werden. Diese Steigerungsbeträge sind nur dann möglich, wenn bedingt durch die Belastungsart und Bauteilgeometrie (Kerben) steile Spannungsgradienten vorliegen und keine festigkeitsmindernden Inhomogenitäten vorhanden sind. Bei dickwandigen Gussbauteilen sind daher zum Beispiel durch Kugelstrahlen weitaus geringere Steigerungen zu erwarten. Die Effektivität der Strahlbehandlung hängt von der Abstimmung der Prozessparameter mit dem jeweiligen Werkstoff und der Bauteilgeometrie ab. Ungänzen oder Entartungen, die im Fertigungsprozess im Werkstoff entstehen können, wirken sich ebenfalls auf das Schwingfestigkeitsverhalten aus [205]. Die Zusammenhänge von zulässiger Beanspruchung in Abhängigkeit vom Gefügezustand, Oberflächenbeschaffenheit und Ungänzen oder Entartungen sind für dickwandige Bauteile aus EN-GJS-400-15 in [206] ausführlich dargestellt.
In der Großserienfertigung von Gussbauteilen gibt es auch andere, wirkungsvollere Möglichkeiten, die Schwingfestigkeit zu steigern, so durch Festwalzen, Induktionshärten oder durch eine Kombination von beiden Behandlungsarten. Je nach Werkstoff, Geometrie und Belastung (wechselnd oder schwellend, konstante oder variable Amplituden) können hierdurch Steigerungen bis etwa Faktor 2,5 in der ertragbaren Spannungsamplitude erreicht werden [207]. Dominiert wird diese Steigerung durch die verfahrensabhängig eingebrachten Druckeigenspannungen in die Randschicht. Durch diese Maßnahmen kann die Schwingfestigkeit häufig wirksamer gesteigert werden als durch konstruktive Maßnahmen.
Grundsätzlich sind alle Randschichtzustände in ihrer Auswirkung auf die Schwingfestigkeit unter dem Gesichtspunkt „fertigungsinduzierter“ (Fräsen, Drehen, Schleifen, usw.) Eigenspannungen zu bewerten.
Belastung
Neben den aufgebrachten äußeren Beanspruchungen (konstante oder variable Amplituden, einachsige oder mehrachsige Belastung) zählen hierzu auch die Umgebungseinflüsse wie Temperaturoder Medieneinflüsse. Unter langen Haltezeiten können bei stationärem Betrieb bei hohen Temperaturen zusätzlich auch Oxidations- und Kriecheffekte auftreten. Für Gusseisen mit Kugelgraphit fällt die Schwingfestigkeit bei höheren Temperaturen ab etwa 100 °C kontinuierlich ab. Gegenüber Raumtemperatur muss bei 300 °C mit rund 10 %, bei 500 °C rund 25 % bis 30 % Minderung gerechnet werden.
Chloridhaltige wässrige Lösungen setzen, je nach Chlorionenkonzentration, die Lebensdauer und die Korrosionsschwingfestigkeit sehr stark herab, da der Abknickpunkt der Wöhlerlinie extrem zu höheren Schwingspielzahlen hin verschoben wird. Unter Schwellbelastung sind die durch korrosives Umgebungsmedium hervorgerufenen Schwingfestigkeitsverluste niedriger als unter Wechselbelastung. Inwiefern Beschichtungen, wie zum Beispiel Verzinken, ein effektiver Schutz gegen Korrosionsermüdung sein kann, muss im Einzelfall untersucht werden.
Eine weitere Korrosionsart unter zyklischer Belastung ist die Reibkorrosion, die häufig aufgrund von Relativbewegungen zwischen Werkstoffpaarungen auftritt. Grundsätzlich verhalten sich Eisengusswerkstoffe hinsichtlich der Reibkorrosion wegen der Schmierwirkung der Graphiteinlagerungen günstiger als Stahl. Die Reibkorrosion kann durch Kugelstrahlen (Oberflächenverfestigung und induzierte Druckeigenspannungen) sehr effektiv verringert werden.
Zyklische Kennwerte
Darstellung zyklischer Kennwerte
Die Wöhlerlinie wird doppellogarithmisch als Belastungs- oder Beanspruchungsamplitude (häufig Spannung) über der Lebensdauer (häufig Schwingspielzahl) aufgetragen, wobei für die Lebensdauer ein Versagenskriterium (Bruch, Anriss einer definierten Größe, Steifigkeitsabfall, usw.) definiert werden muss. Die maßgeblichen Einflussparameter sind der Werkstoff, die Formzahl Kt (sofern deren Definition möglich
ist), das Belastungs- oder Beanspruchungsverhältnis R = Xmin / Xmax (Information über den Mittelwert, dem sich die Amplitude überlagert), die Belastungsart (axial, Biegung, Torsion) und die Umgebung (Temperatur, Medien). Belastungen sind einwirkende Größen wie Kraft, Moment, Druck, oder die am Bauteil entstehenden Größen (Beanspruchungen) wie Dehnung, Spannung oder Verformung (Bild 170).
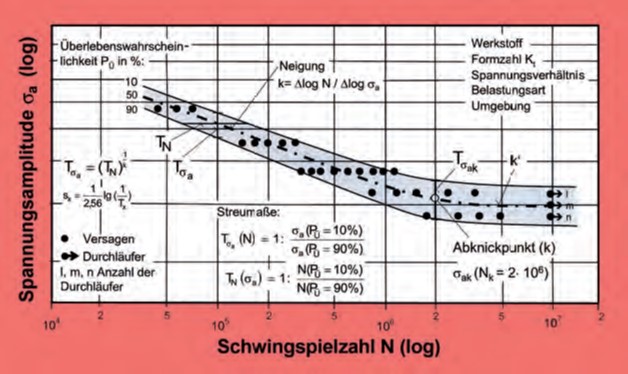
Die Parameter zur Beschreibung einer Wöhlerlinie sind die Neigung k im Bereich der Zeit- oder Kurzzeitfestigkeit, der Abknickpunkt Nk, die Beanspruchbarkeit am Abknickpunkt (z.B. σak) und die Neigung k’ nach dem Abknickpunkt. Diesen zugeordnet ist eine Überlebens- oder Ausfallwahrscheinlichkeit PÜ oder PA. Die Höhe und Lage des Abknickpunktes sowie Neigungen sind abhängig von den oben genannten Einflussparametern. Bei GJSWerkstoffen liegt der Abknickpunkt überwiegend bei N = 2·106 Schwingspielen. Die Streuung der Ergebnisse T ist werkstoff- und fertigungsabhängig und für eine Sicherheitsbetrachtung, die häufig auf der logarithmischen Normalverteilung basiert, notwendig. Unter dieser Annahme lässt sich aus dem Streumaß T, definiert als der Bereich zwischen den Überlebenswahrscheinlichkeiten PÜ=10 % und 90 %, TX = 1 : X(PÜ=10 %) / X(PÜ=90 %), die Standardabweichung berechnen (Bild 170). Im Bereich der Zeit- und Kurzzeitfestigkeit sind die Streumaße TN und Tσa über die Neigung k miteinander gekoppelt. Diese Streumaße werden bis zum Abknickpunkt mit zunehmender Lebensdauer größer. Wegen des flachen Verlaufes der Wöhlerlinie nach dem Abknickpunkt macht die Angabe einer Streuung der Lebensdauer N für den Bereich N > Nk keinen Sinn mehr und ist daher auf die Streuung der Belastungs- oder Beanspruchungsamplitude beschränkt. Sie wird nicht größer als die Streuung im Übergangsbereich von der steilen zur flachen Neigung der Wöhlerlinie. Das im Bereich der Zeitfestigkeit kurz vor dem Abknickpunkt ermittelte Streumaß kann nach dem Abknickpunkt somit als konstant angenommen werden. Diese Annahme ist sinnvoll, weil das Treppenstufenverfahren sowie seine Modifikationen, die zur Bestimmung ertragbarer Last-, Dehnungs- oder Spannungsamplituden für eine festgesetzte Grenzschwingspielzahl am oder nach dem Abknickpunkt verwendet werden, nur einen zuverlässigen Mittelwert, aber kein zuverlässiges Streumaß liefern.
Die genannten Parameter gelten sinngemäß auch für die Ermittlung und Beschreibung von Gaßnerlinien (Kennzeichnung durch „ “ und bedeutet „Höchstwert der Beanspruchung“). Bei Gaßnerlinien sind die Streuungen geringer als bei Wöhlerlinien und je nach Kollektivform verlaufen sie flacher (k ≥ k). Beide werden allgemein als Lebensdauerlinien bezeichnet. Erst im doppellogarithmischen Netz ergeben sich bei deren Darstellung die geradlinigen Verläufe mit den Neigungen k, k’ oder k. Auf der Belastungs- und Beanspruchungsachse werden in der Regel Amplituden aufgetragen. Ein eventuell überlagerter Mittelwert geht aus dem RWert hervor.
Beim Ermitteln von Gaßnerlinien muss eine Teilfolge, beispielsweise als Spitzenwertfolge mit definiertem Teilfolgenumfang, vorliegen. Ein Belastungskollektiv ist die Summe der ertragenen Teilfolgen. Die Versuche werden auf unterschiedlichen Belastungshorizonten durchgeführt, wobei sich die Anzahl der Wiederholungen der Teilfolge und die Größe der Amplituden horizontabhängig ändern. Ein höherer Horizont bedeutet lediglich eine lineare Vergrößerung, ein niedrigerer eine lineare Verkleinerung aller Amplituden und der zugehörigen Mittelwerte (Bild 171). Eine Teilfolge muss, um einen betriebsähnlichen Ablauf abzubilden (betriebsähnliche Durchmischung), mindestens 5 bis 10- mal bis zum Versagen wiederholt werden.
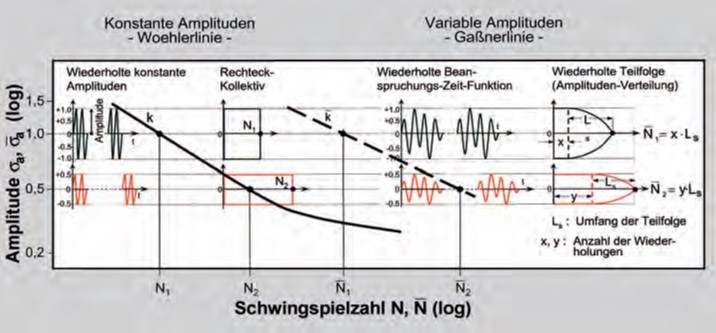
Die Ergebnisse der Gaßnerversuche werden (zumindest im deutschsprachigen Raum) als Amplitudenhöchstwert der jeweils verwendeten Teilfolge über der sich ergebenden Schwingspielzahl beim Versagen aufgetragen. Unter Berücksichtigung des R-Wertes ermöglicht dies einen Vergleich mit der statischen Beanspruchbarkeit, zum Beispiel Werkstoff- oder Formdehngrenze. Darüber hinaus ist erkennbar, um wie viel der Höchstwert den Abknickpunkt der Wöhlerlinie (die sogenannte Dauerfestigkeit) überschreitet. Die genaue Lage von Gaßnerlinien in Abhängigkeit der verwendeten Teilfolge kann theoretisch über Schadensakkumulation berechnet, zuverlässig aber nur durch Versuche bestimmt werden.
Dehnungswöhlerlinien
Zum Bewerten des Werkstoffverhaltens für Beanspruchungen, die die Streckgrenze überschreiten können oder unter wiederholten elasto-plastischen Beanspruchungen ist die Kenntnis der zügigen und zyklischen Spannungs-Dehnungskurven und von dehnungsgeregelt aufgenommenen Anrisswöhlerlinien erforderlich. Sie sind eine Basis für die Bauteilbemessung nach dem örtlichen Konzept. Mit ungekerbten Proben wird das zyklische Verhalten im Kerbgrund von Bauteilen durch die Dehnungsregelung, die auch in hochbeanspruchten Bereichen von Bauteilen aufgrund von Spannungsgradienten vorherrscht, simuliert. Die Koeffizienten und Exponenten nach Coffin-Manson-Basquin, mit denen die Dehnungswöhlerlinie beschrieben wird, sowie der Koeffizient und Exponent nach Ramberg-Osgood für die zügige und zyklische Spannungs-Dehnungskurve finden Eingang in kommerzielle Bemessungsprogramme. Die Gegenüberstellung der zügigen und zyklischen Spannungs-Dehnungs-Kurven zeigt, ob ein Werkstoff bei wiederholter elasto-plastischer Beanspruchung Festigkeit aufbaut (zyklische Verfestigung), abbaut (zyklische Entfestigung) oder sich neutral verhält. Diese Kurven werden außerdem für die Berechnung von Kerbgrundbeanspruchungen, zum Beispiel durch die Anwendung der Neuber-Regel oder deren Modifikationen, verwendet [208]. In der Regel weisen Eisengusswerkstoffe eine zyklische Verfestigung auf.
Bedeutung der Versuche mit variablen Amplituden
Die Bedeutung der Versuche mit variablen Amplituden liegt darin, dass sich gegenüber konstanten Amplituden, bei gleichem Höchstwert eine deutlich höhere Lebensdauer ergibt. Dies ist darauf zurückzuführen, dass die kleineren Amplituden im Gaßnerversuch weniger schädigen als die ständig mit gleicher unveränderter Größe auftretenden Amplituden des Wöhlerversuchs. Um wie viel sich die Lebensdauer im Gaßnerversuch gegenüber dem Wöhlerversuch vergrößert, hängt von der verwendeten Teilfolge ab.
Im Falle einer Geradlinienverteilung (GV) ist der Anteil von kleineren Amplituden im Vergleich zur Normalverteilung (NV) größer (Bild 172).
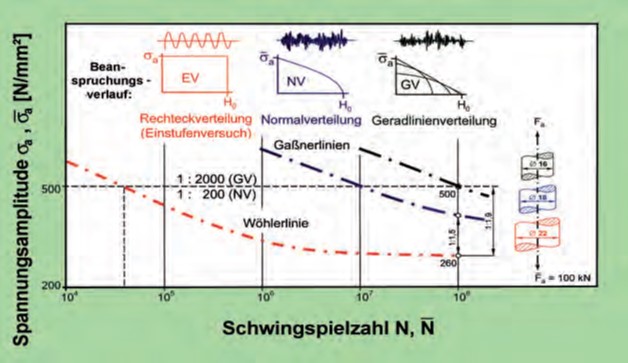
Entsprechend weist die zugehörige Gaßnerlinie eine höhere Lebensdauer auf. Dieser Vorteil über die Kenntnis der Kollektivform und ihrem Einfluss auf die Lebensdauer bei gegebener Belastung lässt sich auch bei der Bauteildimensionierung ausnutzen. Wenn beispielsweise für eine Spurstange eines Fahrzeuges eine Lebensdauer von 108 Schwingspielen erforderlich und die Höchstbelastung Fa = 100 kN durch Betriebsmessungen bekannt ist, kann aus der Wöhlerlinie mit der ertragbaren Spannungsamplitude von σa = 260 N/mm² ein Durchmesser von d = 22 mm berechnet werden. Da aber eine Spurstange im Betrieb Belastungen mit variablen Amplituden ausgesetzt ist (Messungen belegen im vorliegenden Fall eine Geradlinienverteilung), kann bei Kenntnis der entsprechenden Gaßnerlinie für eine Lebensdauer von 108 Schwingspielen die ertragbare Spannungsamplitude von σa = 500 N/mm² als Kollektivhöchstwert zugrunde gelegt und damit ein Durchmesser von d = 16 mm berechnet werden. Diese Querschnittsverringerung wird durch das Zulassen einer Überschreitung der Wöhlerlinie bei 108 Schwingspielen um den Faktor 1,9 ermöglicht. Die Reduzierung des Querschnittes von 22 auf 16 mm bedeutet gleichzeitig eine Verringerung des Gewichtes für diesen Bauteilbereich um Faktor 1,9. Diese Berücksichtigung von zeitlich veränderlichen Amplituden in der konstruktiven Praxis ist der Verdienst von E. Gaßner (1939) und der bedeutendste Fortschritt in der Bauteilbemessung nach A. Wöhler (1866).
Größeneinfluss und Übertragbarkeit
Der Größeneinfluss, ein wesentlicher Faktor bei der Übertragung von an Proben ermittelten Schwingfestigkeitskennwerten auf Bauteile, lässt sich in einen technologischen, spannungsmechanischen, statistischen und oberflächentechnischen Größeneinfluss einteilen, wobei jedoch nicht immer eine vollständige Entkoppelung aller Größeneinfluss-Mechanismen möglich ist [209]. Eine ingenieurmäßige Möglichkeit der Berücksichtigung ist durch das höchstbeanspruchte Werkstoffvolumen gegeben, in dem der spannungsmechanische und der statistische Größeneinfluss zusammenwirken. Es wird vom Spannungsgradienten, der Geometrie und auch von der Art der Belastung (zum Beispiel Planbiegung oder Umlaufbiegung, Axialbelastung, Torsion) bestimmt und beeinflusst somit die Versagenswahrscheinlichkeit entscheidend. Der sogenannte technologische und oberflächentechnische Größeneinfluss ist durch gesonderte Betrachtung von Oberflächen-, Randschicht- und Gefügezustand zu berücksichtigen.
Da Versagen auslösende Werkstoffungänzen sich nicht nur auf die Oberfläche beschränken, sondern sich auch im oberflächennahen Bereich befinden können, hat es sich als brauchbar erwiesen, jenes Volumen, in dem die maximale örtliche Beanspruchung um 10 % abfällt (in dem also mindestens 90 % der maximalen örtlichen Beanspruchungen herrschen), als das höchstbeanspruchte Werkstoffvolumen V90% zu efinieren und zur Bewertung heranzuziehen. Je größer das höchstbeanspruchte Volumen ist, umso größer ist die Wahrscheinlichkeit, dass ein Werkstofffehler anrissinitiierend wirkt. Aus diesem Grunde werden örtlich ertragbare Spannungen von größeren höchstbeanspruchten Werkstoffvolumina geringer. Bei der Übertragbarkeit wird zunächst vorausgesetzt, dass Werkstoff, Oberflächen- und Randschichtzustand einschließlich eventuell vorhandener Eigenspannungszustände von Probe und Bauteil gleich sind. Das heißt, der technologische und oberflächentechnische Größeneinfluss wird berücksichtigt. Die Berücksichtigung des höchstbeanspruchten Werkstoffvolumens ist für dickwandigen EN-GJS-400-15 in [206] beschrieben.
Bauteilbemessung
Bei der Gestaltung eines Gussteils lassen sich mehrere Aspekte gleichzeitig realisieren. Durch das Urformverfahren kann der Konstrukteur ein Gussteil entsprechend den Anforderungen aus Belastung und Geometrie zunächst frei gestalten, wobei hoch beanspruchte Bauteilbereiche immer ein einwandfreies Gefüge aufweisen müssen. Die optimale Gestaltung eines Gussteils erfordert daher bereits in der Entwurfsphase die enge Zusammenarbeit von Konstruktion, Berechnung (numerische Simulation) und Gießerei, damit Gestaltung, Belastung und Gießbarkeit sich nicht widersprechen, sondern ergänzen.
Regelwerke und Normen
Stellvertretend sei hier die FKM-Richtlinie genannt [26], die allgemein für Maschinenbauteile gilt und somit umfassend einen großen Bereich abdeckt. Sie ermöglicht einen Betriebsfestigkeitsnachweis für Bauteile des Maschinenbaus unter Beachtung aller wesentlichen Einflussgrößen. Sie ist ein umfassendes Regelwerk, das in Deutschland und anderen europäischen Ländern anerkannt wird. Es existieren Software-Programme, die die Handhabung beim Nachweis erheblich erleichtern.
Um einer Vielzahl von Anwendungsfällen Rechnung zu tragen, müssen Regelwerke und Normen allgemein formuliert sein. Dies kann zur Überdimensionierung führen, da Bauteileigenschaften bei einer Bemessung nicht zufriedenstellend ausgereizt werden können.
Eingangsgrößen für die Bemessung
Beim Bemessen und Gestalten von gegossenen Komponenten müssen die Funktionalität und das betriebssichere Verhalten möglichst bei minimalem Werkstoffvolumen gewährleistet sein. Die besten Beispiele liefert hierzu die Natur. Doch lassen sich bei der Gestaltung nicht immer (bei Gussteilen aber häufig) die Prinzipien eines „Bio-Designs“ auf eine Konstruktion übertragen, da geometrische Zwänge oft keinen Freiraum zur Gestaltung lassen. Für die Bemessung müssen als Eingangsgrößen viele Randbedingungen bekannt sein, wie zum Beispiel
- Belastungen (Kräfte, Momente, Drücke usw.) oder Beanspruchung (Spannungen oder Dehnungen, einschließlich Medien und Temperatur) in Höhe und Häufigkeit (Lastkollektiv) und deren Eintrittswahrscheinlichkeit;
- Beanspruchbarkeit in Form von Lebensdauerlinien;
- Bemessungslebensdauer und Ausfallwahrscheinlichkeit.
Hierbei sind die kundenspezifischen Beanspruchungsprofile von besonderer Bedeutung. Diese lassen sich am zutreffendsten durch Messungen ermitteln, welche noch unter Berücksichtigung nicht gemessener, physikalischer Randbedingungen aufbereitet werden können. Der Betriebsfestigkeitsnachweis gestaltet sich vielfältig, und reicht vom Nachweisversuch am Bauteil (Bild 174) bis hin zum rein rechnerischen Nachweis [26].
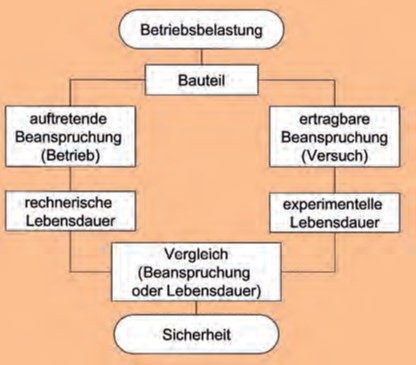
Bemessungskonzepte
Die Kriterien für eine zutreffende betriebsfeste Bauteilbemessung sind die Zuverlässigkeit der Komponenten einer Konstruktion oder des ganzen Systems (Funktionstüchtigkeit) und die Sicherheit (kein Ausfall vor Erreichen der Bemessungslebensdauer für eine geforderte rechnerische Ausfallwahrscheinlichkeit). Folgende Bemessungskriterien werden in der Technik angewendet (Bild 175):
- Statische Bemessung (in der Regel gegen die Werkstoff-Dehngrenze);
- „Dauerfeste“ (sogenannte) Bemessung, wenn das Kollektiv unterhalb des Wöhlerlinienverlaufes nach dem Abknickpunkt liegt, aber der Kollektivhöchstwert weitaus mehr als 106 mal auftritt (Dies ist zum Beispiel bei Pleueln, Kurbelwellen und Zahnrädern der Fall). Obwohl die Belastungen mit variablen Amplituden auftreten, werden sie wegen der hohen Häufigkeit des Kollektivhöchstwertes wie eine Belastung mit konstanten Amplituden behandelt;
- „Betriebsfeste“ (sogenannte) Bemessung, wenn eine Überschreitung des Wöhlerlinienverlaufes nach dem Abknickpunkt durch den Kollektivhöchstwert sowie durch eine begrenzte Anzahl von variablen Amplituden erlaubt wird. Die Zulassung höherer Beanspruchungen als beim Abknickpunkt der Wöhlerlinie führt zu kleineren Bauteilquerschnitten (Leichtbau!).
Die folgenden Konzepte werden in den verschiedenen Sparten der Technik, manchmal gleichzeitig, angewendet.
1. Nennspannungskonzept - Das Nennspannungskonzept setzt die Definition sowohl einer Nennspannung als auch die Zuordnung einer Formzahl beziehungsweise bei Schweißverbindungen einer Kerbfallklasse (Kerbdetail) voraus. Nach der Definition dieser beiden Größen muss eine Bemessungswöhlerlinie im Nennspannungssystem für die gleiche Kerbzahl oder Kerbfallklasse des zu bewertenden Bauteils herangezogen werden. Dieses Konzept, das auch mit Nenndehnungen arbeiten kann, stößt bei komplexen Geometrien, für die weder eine Nennbeanspruchung noch eine Formzahl definiert werden kann, an seine Anwendungsgrenzen. Zudem verdrängen die heutigen Möglichkeiten in der numerischen Simulation, die örtliche Beanspruchungen zur Verfügung stellen, dieses Konzept immer mehr.
2. Strukturspannungskonzept - Das Strukturspannungskonzept wurde für Schweißverbindungen entwickelt. Das Konzept, bei dem auch Dehnungen zugrunde gelegt werden können, extrapoliert die Spannungsverteilung außerhalb der Schweißnaht auf die Nahtübergangskerbe nach festgelegten Kriterien und definiert eine Hot-Spot-Spannung. Diese Spannung wird dann einer Strukturspannungswöhlerlinie zugeordnet und bewertet. Der Vorteil dieses Konzeptes liegt darin, dass bei komplexer Geometrie das Problem der Definition einer Nennspannung, gegebenenfalls auch eines Kerbfalles, umgangen wird. Im Vergleich zum Nennspannungskonzept werden bei Schweißverbindungen sehr wenige Kerbfall-(Detail)klassen angegeben. Der Nachteil liegt darin, dass von außen nicht zugängige kritische Bereiche, wie beispielsweise Wurzelkerben, mit diesem Konzept nicht mehr beurteilt werden können.
3. Örtliches Konzept - Das Örtliche Konzept (Kerbgrundkonzept) kann sowohl mit Spannungen als auch mit Dehnungen arbeiten. Hierzu müssen die lastbedingten Kerbspannungen- oder dehnungen ermittelt werden und für deren Bewertung die örtlich ertragbaren Beanspruchungen (Beanspruchbarkeit), das heißt Lebensdauerlinien im örtlichen System, unter Berücksichtigung des Größeneinflusses, Oberflächen- und Randschichtzustandes, vorliegen. Der Vorteil dieses auch für Schweißverbindungen anwendbaren Konzeptes liegt darin, dass die für das Versagen verantwortlichen lokalen Beanspruchungsgrößen auch für schwierigste Geometrien numerisch ermittelt werden können.
4. Bruchmechanikkonzept - Das Bruchmechanikkonzept geht von der Vorstellung aus, dass in kritischen Bereichen eines Bauteils rissartige Fehler oder Geometrien vorliegen, von denen aus ein Riss eingeleitet werden und fortschreiten kann. Die Risseinleitung kann durch die Definition einer Spannungsintensität, der Rissfortschritt durch zusätzliche Werkstoffgesetze linear-elastisch oder elastoplastisch behandelt werden. Findet die Entstehung eines technischen Anrisses bis zu einer definierten Länge oder Tiefe keine Berücksichtigung, wird bei dieser Bemessungsmethode diese Lebensdauerphase nicht genutzt. Zu dieser Thematik ist bereits ausführlich in Kapitel 8.6 berichtet worden.
5. Versagenshypothesen - Die Beanspruchungen in kritischen Bereichen von Bauteilen sind in der Regel mehrachsig. Sie können nur dann bewertet werden, wenn sie mittels einer geeigneten Festigkeitshypothese in eine Vergleichsspannung umgewandelt werden. Für Eisengusswerkstoffe kann die Schnittebenen bezogene Normalspannungshypothese (NH) sowohl für Beanspruchungen mit konstanten als auch zeitlich veränderlichen Hauptspannungsrichtungen angewendet werden [210 - 212].
6. Lebensdauerabschätzung - Die Frage nach der Lebensdauerabschätzung stellt sich bei zeitlich veränderlichen Beanspruchungen. Zur rechnerischen Abschätzung der Lebensdauer nach der Hypothese der linearen Schadensakkumulation nach Palmgren (1924) – Miner (1945) (Bild 176) ist die Kenntnis des Kollektives (Rainflow-Matrix oder Überschreitungshäufigkeit von Klassengrenzen in Kombination mit der Bereichspaarzählung) und auch der Wöhlerlinie erforderlich.
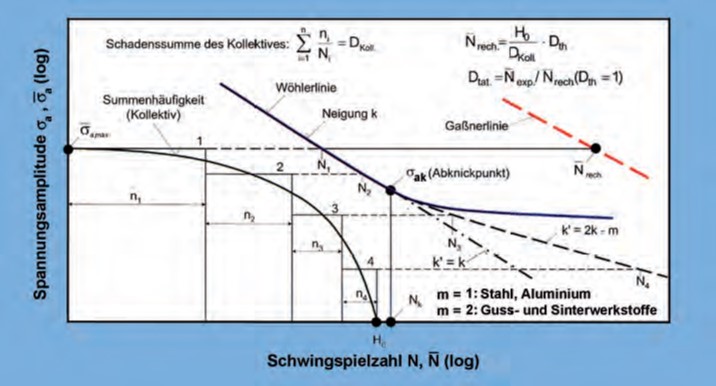
Da die Amplituden des Kollektivs in aller Regel unterschiedliche R-Werte aufweisen, wird häufig eine Transformation auf den R-Wert der Wöhlerlinie vorgenommen. Bei der Original-Palmgren-Miner-Rechnung verläuft die Wöhlerlinie nach dem Abknickpunkt waagerecht. Das heißt, es wird nicht berücksichtigt, dass Amplituden unterhalb des Abknickpunktes schädigen. Aus diesem Grund wird die Wöhlerlinie, je nach Modifikation der Palmgren-Miner-Regel, nach dem Abknickpunkt mit einer veränderten Neigung fortgesetzt, zum Beispiel mit k’=k (Palmgren-Miner-Elementar) oder mit k’=2k - m (Modifikation nach Haibach mit m = 2 für Gusswerkstoffe), um auch der Schädigung durch kleine Amplituden unterhalb des Abknickpunktes Rechnung zu tragen. Die meist angewandten Modifikationen sind die vorstehend genannten. Nach der Summation der Teilschädigungen ni/Ni kann die Lebensdauer Nrech. mit der theoretischen Schadenssumme Dth=1,0 berechnet (abgeschätzt) werden. Für eine zutreffende Abschätzung ist die Kenntnis der tatsächlichen Schadenssumme Dtat. erforderlich, die in der Regel kleiner als 1,0 ist. Sie lässt sich nur aus Experimenten (Wöhler- und Gaßnerlinie) als Verhältnis zwischen der experimentell ermittelten Lebensdauer und der mit Dth=1,0 berechneten bestimmen (Bild 176), und ist mit dem Berechnungsverfahren und Kollektiv verknüpft. Falls im Betrieb andere Kollektivformen vorliegen als die im Versuch verwendeten, kann in diesem Fall die Lage der entsprechenden Gaßnerlinie durch eine relative Schädigungsberechnung abgeschätzt, jedoch seltenst zutreffend berechnet werden. Die tatsächlichen Schadenssummen können über drei Dekaden streuen. Etwa 90 % der aus Experimenten abgeleiteten Schadenssummen liegen unter dem theoretischen Wert Dth=1,0. Das heißt, Berechnungen mit Dth=1,0 liefern in den meisten Fällen eine Überschätzung der Lebensdauer. Aus diesem Grunde wird bei einer Vorbemessung zur Abschätzung der Lebensdauer für Schweißverbindungen die zulässige Schadenssumme Dzul=0,5 und für nicht geschweißte Bauteile Dzul=0,3 (FKMRichtlinie) angenommen. Für Beanspruchungszeit-Abläufe mit hohen Mittelwertschwankungen sollte anstatt 0,5 der Wert 0,2 und anstatt 0,3 der Wert 0,1 verwendet werden. Aufgrund dieser Unsicherheiten ist ein experimenteller Festigkeitsnachweis, sofern dies möglich ist, insbesondere für Sicherheitsbauteile stets zu empfehlen.
Ertragbare Beanspruchungen
Bruchverhalten unter Schlagbelastung
Bei einer betriebsfesten Auslegung müssen Bauteile auch nach Entstehen eines unvorhergesehenen Anrisses einer Missbrauchsbelastung wie einem Schlag durch eine entsprechende Festigkeitsreserve standhalten. Solche Belastungen können zum Beispiel an Fahrwerkskomponenten bei einer Fahrt über ein Hindernis, durch ein Schlagloch oder bei einem Aufprall gegen eine Bordsteinkante auftreten. Ausführlich wurde bereits unter 8.6 auf das Riss- und Bruchverhalten bei statischer, zyklischer und dynamischer Beanspruchung eingegangen.
Im Bild 177 wurden zwei Nutzfahrzeug- Radnaben gleichen Gewichts aus einem geschmiedeten und einem gegossenen Werkstoff gegenübergestellt, bei denen in den höchst beanspruchten kritischen Bereichen künstliche Anrisse mit einer Tiefe von 0,5 mm im hoch beanspruchten Bereich eingebracht wurden. Bei den konventionellen Werkstoffkennwerten zeigt sich zwar der Schmiedestahl dem Gusswerkstoff überlegen, jedoch ist aufgrund der gusstechnischen Gestaltung (Rippen in den kritischen Bereichen) im Vergleich zu der geschmiedeten Nabe eine deutlich höhere Schlagkraft erforderlich, um einen Gewaltbruch zu erzeugen. Die Höhe der unter schlagartiger Belastung erforderlichen Bruchkraft wird im Beispiel stark von der Geometrie beeinflusst und erlaubt daher keine Korrelation mit den an Proben ermittelten statischen Werkstoffkennwerten.
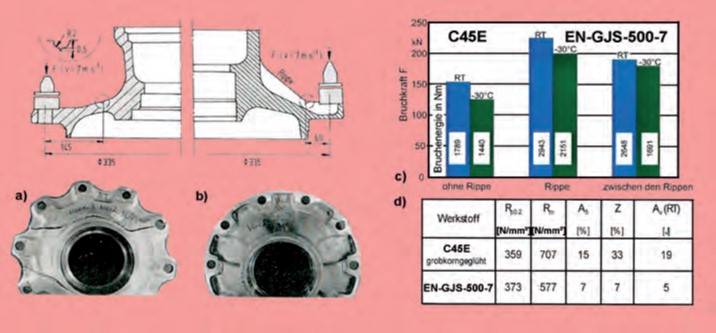
a) geschmiedete Nabe aus C45E
b) gegossene Nabe aus EN-GJS-500-7
c) Bruchkraft
d) mechanische Eigenschaften
Formdehngrenze
Die 0,2-%-Werkstoffdehngrenze (die Spannung mit einer bleibenden (plastischen) Verformung von εpl = 0,2 %) wird mit einem ungekerbten Probestab (Kt = 1,0) im Zugversuch oder während eines dehnungsgeregelten Versuchs aus der Last-(Spannung)-Dehnungskurve ermittelt. Sobald der linear-elastische Bereich der Spannungs-Dehnungskurve überschritten wird, neigt der Werkstoff unter Lastregelung und axialer Belastung, je nach seinen Verfestigungseigenschaften, wegen nicht vorhandener Stützwirkung (kein Spanernungsgradient) zu einem unkontrollierten Fließen. Dies kann bei der ungekerbten Probe nur durch eine Dehnungsregelung (Dehnungswöhlerlinie) unterbunden werden.
Für das Erreichen der 0,2%-Bauteil-Dehngrenze hingegen sind am Bauteil oder an einem Kerbstab, im Vergleich zur 0,2-%-Dehngrenze der ungekerbten Probe, eine höhere örtliche Gesamtdehnung erforderlich. Dies ist durch die Spannungsgradienten in der Kerbe des Bauteils oder der Kerbprobe bedingt. Das Verhältnis zwischen der örtlichen Gesamtdehnung, die am Bauteil und an der ungekerbten Probe eine bleibende Verformung von 0,2-% ergeben, wird als Stützziffer definiert. Die Spannungsgradienten in der Kerbe verhindern örtlich ein unkontrolliertes Fließen, das heißt, sie üben trotz der äußeren Lastregelung örtlich bis zu einem gewissen Maß eine Dehnungsregelung aus, sofern die 0,2-%-Bauteil-Dehngrenze nicht überschritten wird. Deswegen liegt am Bauteil oder an der Kerbprobe zwischen der äußeren Belastung und örtlichen Dehnung ein größerer linearer Bereich vor als bei der ungekerbten Probe. Die aus der Sicht der Betriebsfestigkeit wichtige Bauteil-Formdehngrenze, die durch eine Betriebsbeanspruchung infolge einer Sonderbelastung angesprochen werden kann, darf die Ermüdungsfestigkeit nicht beeinträchtigen. Sie ist daher, je nach Werkstoff und Konstruktion, kleiner als die 0,2-%-Bauteil-Dehngrenze, zum Beispiel 0,02 bis 0,05 %.
Auswahl bemessungsrelevanter Kennwerte
Schwingfestigkeitskennwerte werden überwiegend an Proben ermittelt und zur Verfügung gestellt. Die Aussagekraft dieser Kennwerte hängt davon ab, inwieweit der Anwender anhand der zur Verfügung gestellten Daten in der Lage ist, verschiedene Einflussfaktoren zu bewerten. Weiklärt terhin ist das Versagenskriterium von Bedeutung. Schwingfestigkeitskennwerte, die an ungekerbten Proben ermittelt wurden, bieten meistens einen konservativen Ansatz, da die Proben unter Axialbelastung keinen Spannungsgradienten aufweisen. Unter Biegebelastung werden, in Abhängigkeit des Spannungsgradienten, in aller Regel höhere Kennwerte ermittelt (Bild 178).
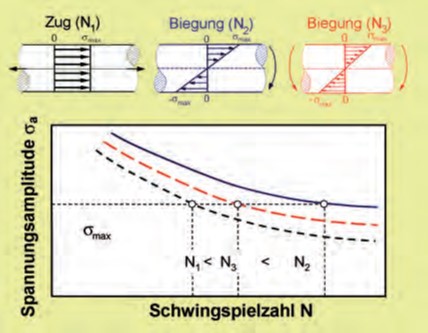
Es ist daher sehr schwierig, Kennwerte wie im Bild 167 zur Verfügung zu stellen, da diese immer eine Bemessungsmethodik erfordern (Berücksichtigung lokaler Eigenschaften wie Gefüge, Festigkeit, Randschichtzustand, höchst beanspruchtes Werkstoffvolumen, Oberflächennachbehandlung, usw.), die die zuverlässige Übertragbarkeit der Kennwerte von Proben auf Bauteile ermöglicht.
Sofern keine Erfahrungen bezüglich der Schwingfestigkeitskennwerte vorliegen, empfiehlt sich immer ein Nachweisversuch mit dem realen Bauteil. Sofern dies nicht möglich ist, sollte mit dem Bauteil entnommenen Proben (keine Angussproben) mit vergleichbaren lokalen Eigenschaften eine Lebensdauerlinie abgeleitet werden.
1. Kennwerte zu dickwandigem Guss
Zyklisch beanspruchte, dickwandige Bauteile aus Gusseisen mit Kugelgraphit, wie zum Beispiel Motorblöcke für Großdieselmotoren, Rahmen für Schmiedepressen, Hydraulikzylinder für Kunststoffspritzgießmaschinen, Verdichter- und Turbinengehäuse, Mahlteller usw., werden oftmals nur in geringen Stückzahlen produziert. Aus diesem Grunde ist es unwirtschaftlich, den Gießprozess wie bei Serienbauteilen hinsichtlich Gießverfahren, Einsatzmaterialien, Metallzusammensetzung, Impfung, Anschnitttechnik usw. zu optimieren. Infolgedessen wird das geforderte Grundgefüge nicht immer über den gesamten Querschnitt erreicht und der Abnehmer akzeptiert das Bauteil meistens nicht. Es wird zu Ausschuss erWeiklärt, wodurch den Unternehmen hohe Kosten entstehen, sowohl durch die erneute Herstellung als auch durch die arbeitsintensive Verschrottung des Ausschussteils. Daher wurden Schwingfestigkeitskennwerte für Ungänzen wie Dross an der Oberfläche, Lunkern im angeschnittenen oder eingebetteten Zustand, Graphitentartungen (zum Beispiel Chunky-Graphit) und verschiedenen anderen Entartungen bereitgestellt, die an großen, teilweise dem Bauteil entnommenen Proben ermittelt wurden (Bild 180).

+) N = 2 . 106 Schwingspiele, höchstbeanspruchtes Werkstoffvolumen HbV = 8000 mm³, Vertrauenswahrscheinlichkeit C = 90 %, Überlebenswahrscheinlichkeit PÜ = 50 % #) Poren, leicht entartetes Gefüge mit Poren, Graphit-Entartungen (Form III), punktueller Dross
Die Kennwerte für Gefüge ohne und mit Entartungen sind derart aufbereitet, dass sie unmittelbar in die Bemessungspraxis des für dickwandige Bauteile häufig verwendeten Gusswerkstoffes EN-GJS-400-15 einfließen können [30, 206]. Aus den ermittelten Schwingfestigkeitskennwerten wurde der Einfluss der Belastungsarten, Geometrien und Spannungsgradienten eliminiert und die Kennwerte bei einer definierten Schwingspielzahl einem bestimmten höchst beanspruchten Werkstoffvolumen zugeordnet. Die ertragbaren Vergleichsspannungsamplituden für Wechsel- und Schwellbelastung lassen sich auf andere höchst beanspruchte Werkstoffvolumina, Schwingspielzahlen und auch Spannungsverhältnisse umrechnen. Über eine Sicherheitsbetrachtung können dann die zulässigen Beanspruchungen, die von den metallographischen Gegebenheiten der zu bemessenden Bauteilbereiche abhängen, den auftretenden gegenübergestellt werden. Dadurch ist eine sofortige Entscheidung über die Freigabe eines Bauteils möglich. Die Methodik ist sowohl bei Gießern als auch bei deren Kunden akzeptiert.
2. Kennwerte zu ADI
Bei gekerbten Bauteilbereichen ist eine Erhöhung der Schwingfestigkeit durch die Wahl eines höherfesten Werkstoffes zunächst nicht zu erwarten (Bild 167). Bereits relativ alte Untersuchungen zeigen aber, dass mit dem Werkstoff ADI (siehe 8.1) durchaus auch bei Kerben eine Erhöhung der Schwingfestigkeit möglich ist, insbesondere wenn variable Amplituden vorliegen (Bild 181).
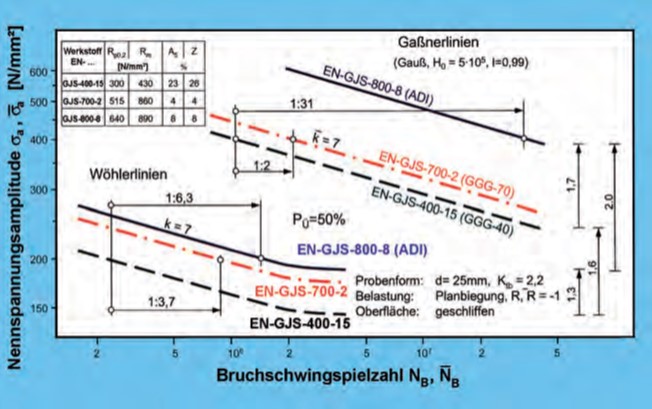
Unter schwellenden variablen Amplituden treten höherfeste perlitische Gusswerkstoffe (Temperguss ENGJMB-700-2 und Gusseisen mit Kugelgraphit EN-GJS-700-2) und auch ADI bereits schon im nicht Randschicht nachbehandelten Zustand in Konkurrenz zu Schmiedestählen [213] (Bild 182).
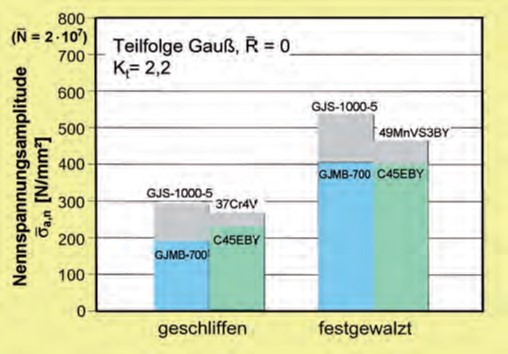
Neuere Untersuchungen [214, 215] verdeutlichen anhand von dehnungsgegegelten Versuchen an ungekerbten Proben das vorhandene Potential. Bei einem Unterschied in den zyklischen Dehngrenzen von 75 % beträgt die reale Steigerung für ADI gegenüber EN-GJS-400-15 100 % unter konstanten Amplituden und 120 % unter variablen Amplituden (Bild 183).
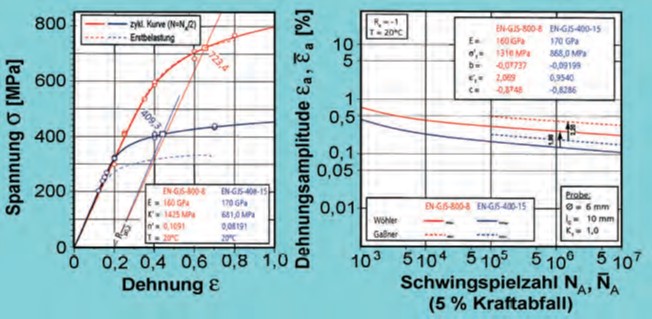
a) Spannungs-Dehnungs-Kurven
b) Dehnungs-Wöhlerlinien und -Gaßnerlinien
Dieses Verhalten wurde auch bei realen Bauteilen (Panhardstäben) mit roher, reinigungsgestrahlter Oberfläche nachgewiesen (Bild 184).
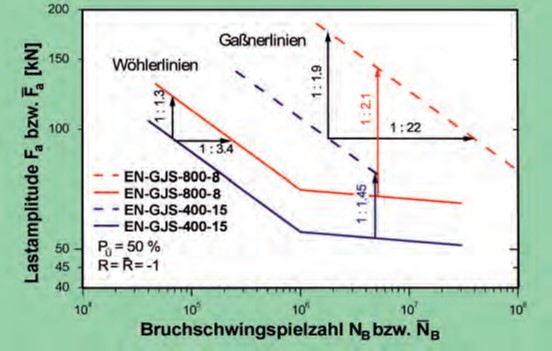
Von diesen Werkstoff mit „austenitischferritischem“ (stabilisierter Austenit mit Ferritnadeln) Gefüge, der durchaus vom SITRAM-Effekt (spannungsinduziert umwandelnder Martensit) profitiert, wurden bisher kleinere Serien zum Anlaufen gebracht. Für einen Großserieneinsatz ist der Bedarf für diesen Werkstoff von der Industrie noch konkret zu formulieren. Ein erfolgreicher Einsatz ist dann möglich, wenn das Einsatzprofil im Einklang mit dem Produkt steht und Grundlagen für eine Bauteilvorbemessung und Lebensdauerabschätzung zur Verfügung gestellt werden.
Sicherheitsbetrachtung
Für eine Bauteilbemessung wird, ausgehend von einer Lebensdauerlinie mit einer Überlebenswahrscheinlichkeit von PÜ = 50 %, eine Bemessungslebensdauerlinie, das heißt die zulässige Schwingfestigkeit, abgeleitet. Hierzu muss, je nach dem Gefährdungspotenzial eines Bauteils, zunächst eine rechnerische (theoretische) Ausfallwahrscheinlichkeit PA definiert werden: Bei lebenswichtigen Bauteilen, die niemals ausfallen dürfen, wie Bremsen zum Beispiel PA ≤ 10-6, bei Bauteilen, die häufig inspiziert und in einem abgesicherten Bereich betrieben werden (zum Beispiel ein Hochdruckbehälter in einem Bunker) PA = 10-3.
Weiterhin müssen bekannt sein:
sX - Standardabweichung um den Mittelwert (PÜ = 50 %) der Beanspruchbarkeit X (X - ertragbare Beanspruchung, wie z. B. Spannung, Dehnung, Kraft, Moment, Druck) mit
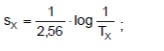
sM - Standardabweichung des Mittelwertes der Beanspruchbarkeit (chargenoder fertigungsbedingte Streuungen des Mittelwertes im Rahmen der Qualitätskontrolle);
sB - Standardabweichung der Beanspruchung (Belastung) (Falls die maximale Belastung als bekannt vorausgesetzt werden kann, folgt sB = 0).
Unter der Annahme einer logarithmischen Normalverteilung kann aus den einzelnen Standardabweichungen die Gesamt-Standardabweichung
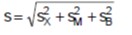
berechnet werden [216].
Aus der festgelegten rechnerischen Ausfallwahrscheinlichkeit und der Gesamt-Standardabweichung berechnet eine praxistaugliche Näherungslösung [217] den Sicherheitsfaktor
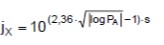
ausreichend genau. Die zulässige Beanspruchung für die geforderte rechnerische Ausfallwahrscheinlichkeit ergibt sich zu
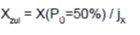
Bei Schwingspielzahl abhängigen Streuungen ergeben sich entlang der Lebensdauerlinie (PÜ = 50 %) unterschiedlich große Sicherheitsfaktoren für die Ableitung der Bemessungslebensdauerlinien.
Die Betonung auf ‘rechnerisch’ ist dadurch begründet, dass der tatsächliche Verlauf einer Verteilung außerhalb des Bereiches PÜ ≈ 5 bis 95 % nicht bekannt ist. Trotzdem ist der Ansatz von rechnerischer Ausfallwahrscheinlichkeit berechtigt, wenn seine Festlegung sich auf nachweisbare Erfahrungen bezüglich eines ausfallfreien Betriebes der Komponenten stützt.
Zur Ableitung von Sicherheitsfaktoren können auch andere Verteilungsformen, zum Beispiel Weibull, verwendet werden. Auch hierfür müssen entsprechende Betriebserfahrungen vorliegen.
Nachweisversuche
Grundsätzlich müssen Bauteile so bemessen werden, dass die geforderte Lebensdauer ohne Ausfall erreicht wird. Diese Forderung kann, je nach Relevanz der Bauteile, durch unterschiedliche Qualitäts- und Wirtschaftlichkeitsmaßstäbe erfüllt werden, die von der Einteilung in Primärkomponenten und Sekundärkomponenten nach den Gesichtspunkten der Sicherheit und Funktionstüchtigkeit abhängt. Hierbei werden Primärkomponenten in Sicherheits- und Funktionskomponenten unterteilt.
Bei Sicherheitskomponenten, wie zum Beispiel Schwenklager und Räder, muss ein Versagen ausgeschlossen werden, weil dies Lebensgefahr für den Nutzer und die Umgebung bedeutet. Bei solchen Bauteilen werden bei der Bemessung hohe Sicherheitsfaktoren zugrunde gelegt. Bei Funktionskomponenten wird die Vermeidung eines Versagens ebenfalls angestrebt, da die Funktion der Bauteilgruppe unterbunden wird (zum Beispiel Pleuel oder Kurbelwelle). Bei Sekundärkomponenten hingegen, wie Auspuffkrümmer, hat ein Schaden meistens keine direkte Auswirkung auf die Sicherheit und Funktionstüchtigkeit. Demzufolge werden bei Primärkomponenten höhere Qualitätsanforderungen gestellt, auch wegen den wirtschaftlichen Folgen bei einem Versagen. Zum Beispiel muss bei lebenswichtigen Sicherheitskomponenten die Bemessung alle im Betrieb auftretenden Belastungen nach dem stets neuesten Stand der Technik und der Wissenschaft abdecken. Hierzu sind nicht nur die genaue Erfassung der Betriebsbelastungen erforderlich, sondern auch die Kenntnis der versagenskritischen Bereiche des Bauteils und die örtliche Anstrengung (Verhältnis zwischen der auftretenden und vom Werkstoff oder der Fertigungstechnologie abhängigen zulässigen Vergleichsbeanspruchung). Danach kann die tolerierbare Qualität des Bauteils unter Gesichtspunkten der Wirtschaftlichkeit festgelegt werden.
Qualitätsforderungen, die an die Sicherheit eines Bauteils gekoppelt sind, können nur durch entsprechende Nachweisversuche unter Simulation realer Betriebsbedingungen oder Fahrversuche gewährleistet werden, mit denen die kritischen Bereiche und die Art des Versagens erkannt werden müssen. Ein weiterer Vorteil der Festigkeitsversuche liegt darin, dass durch sie die Konstanz der Fertigungsqualität unter Anwendung statistischer Methoden ständig überprüft werden kann, wie dies beispielsweise in der Pleueloder Kurbelwellenherstellung der Fall ist. Der Festigkeitsnachweis muss durch entsprechende Qualitätsvorschriften in der Konstruktion, Materialbeschaffung und Fertigung gestützt werden. Messungen von Betriebsbeanspruchungen zur Verifizierung und gegebenenfalls rechtzeitigen Korrektur der Berechnungen sollten soweit wie möglich vorgesehen werden. Zur Verkürzung der Versuchszeiten kann, unter Berücksichtigung der jeweiligen Amplitudenmittelwerte, eine Omission (Weglassen kleiner Schwingspiele, die nicht zur Schädigung beitragen) durchgeführt werden. Bei mehrachsigen Versuchen ist die Interaktion der einzelnen Zeitsignale zu berücksichtigen [218].
Weiterführende Informationen zum Werkstoff Gusseisen mit Kugelgraphit
- Hier geht es zu den allgemeinen Informationen: Gusseisen mit Kugelgraphit | GUSS
- Hier finden Sie Informationen zur Wärme- und Oberflächenbehandlung: Wärme- und Oberflächenbehandlung | GUSS
- Hier finden Sie Informationen zur Werkstoffprüfung: Werkstoffprüfung | GUSS
- Hier finden Sie Informationen zur Spanenden Bearbeitung: Spanende Bearbeitung | GUSS
- Hier finden Sie Informationen zu besonderen Eigenschaften: Besondere Eigenschaften | GUSS
Download
Autoren und Quellen
Autoren:
Dr. Ch. Bartels, DI R. Gerhards, Prof. H. Hanselka, Prof. K. Herfurth, Dr. H. Kaufmann, DI W. Kleinkröger, Dr. M. Lampic, Dr. H. Löblich, Dr. W. Menk, Prof. G. Pusch, Dr. T. Schmidt, DI K.-H. Schütt, DI P. Tölke, Prof. E. P. Warnke





